Eighteenth Century British aestheticians, notably Hutcheson and Gerard, make much of the formula: uniformity amidst variety. Often these terms do duty for a larger set including “regularity,” “simplicity,” “complexity,” “intricacy,” “number,” “proportion,” “order” and “congruity.” “Beauty,” says Gerard, “belongs to objects possessed of uniformity, variety and proportion. Each of these qualities pleases in some degree; but all of them united give exquisite satisfaction.” (Gerard 29) So stated it appears that beauty – intrinsic beauty -- depends on purely objective properties.

On the other hand we also find a quite different, emphatically psychological explanation of what we count as beautiful. “Objects endued with these qualities enter easily into the mind…each part is distinctly and strongly conceived: the view of a part suggests the whole, and, impelling the mind to imagine the rest, produces a grateful exertion of its energy.” (29-30) But uniformity if “perfect and unmixed… cannot…alone produce pleasure, either very high, or of very long duration…Variety in some measure gratifies the sense of novelty, as our ideas vary in passing from the contemplation of one part to that of another. This transition puts the mind in action, and gives it employment, the consciousness of which is agreeable.” (31) On the other hand, “Were the variety indeed boundless, the mind would be fatigued and pained with continual shifting from part to part, without the prospect of any end to its labors.” Thus “a certain degree of uniformity must be blended with the variety of objects…” in order that the mind obtain “the opposite gratifications of facility and active exertion, mixed with, and mellowing one another.” (33) So stated the rule seems to be to find the sorts of uniformity and variety that combine to produce high and lasting pleasure: uniformity and variety recipes, so to speak. What was earlier presented as the payoff of beauty begins to seem a coordinate or perhaps governing criterion. The latter would fall into line with the idea of beauty as a response-dependent property, as befits the sense of beauty tradition. 1

Thus we have both an objective and a psychological criterion. On the one side intrinsic beauty consists in: combinations, mixtures, blendings of uniformity, variety, proportion, order, simplicity, intricacy, etc.

On the psychological side beauty consists in visual comprehensibility and visual interest 2, these being necessarily subject to the constraints of our perceptual and cognitive systems, which cannot handle excessive complexity, multiplicity and subtlety, on the one hand, or excessive simplicity and uniformity on the other .

My purpose here is to explore the concepts cited above with particular reference to a set of examples that prima facie represents the most comprehensible application. I will also briefly comment on the relation between the objective and the psychological criteria. 3

1

First we need to sort out the meanings of the most fundamental of the terms in the 18 th century list.. “Regularity” is standardly defined in terms of the uniformity of “parts,” and different grades of regularity are explained as degrees of uniformity. Uniformity is defined as similarity, 4 variety as dissimilarity, of correspondent parts. 5 On this basis a rectangle is less regular than a square because, while its angles are all equal, its pairs of correspondent sides are of different lengths. The rhombus distributes uniformity differently. Its sides are equal in length and variety appears in its angles, which divide 2 by 2.

As it plain from these examples, uniformity and variety are relative to a given property. If relative to the same property then they are plain contraries. If relative to logically independent properties they are compatible, that is, logically independent.

Such independence is crucial to Hutcheson's idea of blending uniformity and variety: where the uniformity of two things A and B is equal but one, B say, has more variety than the other, that one, B, has the better blend of the two qualities. This wouldn't make sense unless the respects in which A and B are diverse were logically independent of those in which they are uniform.

Complicating the scene here is the fact that Hutcheson understands variety in terms of number. This is puzzling because the number (of sides or angles, for instance) doesn't seen related to diversity or dissimilarity at all.

Further when it comes to ranking polygons with a given number of sides, quadrilaterals, say, the measure Hutcheson uses is uniformity, not variety. The rectangle's variety of side-length does not count in its favor. No, it only makes it less uniform and therefore less beautiful than the square.

I will shortly propose a friendly revision of Hutcheson's uniformity and variety rule that reconciles variety as diversity with variety as number. But this is not needed for the first of Hutcheson's two rankings of polygons, where regular polygons are compared with members of their polygon set: the regular pentagon with pentagonals, for example. As just mentioned, here only uniformity counts. The relevant parts are the sides and the angles, if we judge by what Hutcheson says. He omits to consider, what is certainly essential to the topic, the grade of symmetry possessed by a figure. Regular polygons possess as many angles of rotational symmetry and as many axes of reflective symmetry as is possible for their kind – which ultimately means, for the number of sides they possess.

Figure 1 sets forth an essentially Hutchesonian ranking for four and five-sided polygons, regular and non-regular. I have to add that qualifier because Hutcheson doesn't assign numerical values or in general deal with important matters of detail. For example, my ranking relativizes the scoring to the number of sides, the principle being to rank a given item within its set by the degree to which it approaches the maximum of its kind. But I doubt that Hutcheson would take exception to this approach once he thought it over. I also doubt he would object to the specific rankings, which correspond pretty well with his. For his view is explicitly that the regular polygons are more uniform, and therefore more beautiful, than the others in proportion to the difference of uniformity 6 .

Figure 1 .

(Note that each figure numbered .2-.5 stands for a class of figures possessed of the indicated distribution of side-to-side and angle-to-angle relations. The values given for each class are constant for all of its members. But of course they do not exhaust the variables bearing on overall regularity.)

2

When it comes to Hutcheson's second ranking, where regular polygons are put head to head with each other, variety plays a central role. As previously mentioned his declared candidate for variety is number, in this case number of sides, not diversity (dissimilarity). But he also holds that the non-parallelism of sides in odd-sided polygons reduces their uniformity compared with the even-sided ones, whose opposite sides are parallel. This is a case of the odd-sided polygons possessing variety in the sense of diversity, that is, non-uniformity. He doesn't say how much this specific non-uniformity lowers the rating of a regular polygon. Perhaps it lowers a pentagon to the level of a square, or perhaps not quite that much. In either case the step from pentagon to hexagon is enlarged.

Aside from that factor, the ranking of regular polygons by Hutcheson depends simply on the number of sides, at least until psychological limits are transgressed. Figure 2.

That's Hutcheson's view. Which of us today would lend it credence? I think none. No one thinks a nonagon (9-sided) is more beautiful than a hexagon because it has three more sides. But if that's not the basis for relating the two, what should it be?

For years I thought no valid ground existed for ranking regular polygons in terms of uniformity and variety. But now I believe there are solid grounds for just such a ranking (or at least for partial rankings). At the very least we can see how to specify the concepts of uniformity and diversity so as to construct a ranking in a Hutchesonian vein.

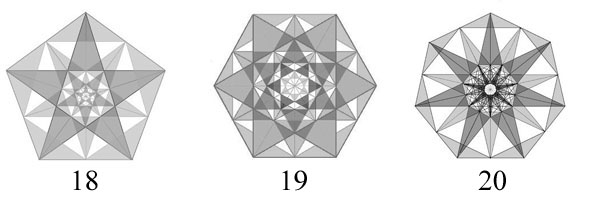
The breakthrough comes via recognition of the content of a polygon. This lifts us out of the paralysis induced by mere contemplation of the outlines of the polygons. No amount of earnest contemplation of Figure 2 will yield the required enlightenment. The way forward is to study differences of content.

By content I mean the forms within a polygon that are essential to its being the polygon it is. Content is revealed when the foundational nodes of the outline, specifically the vertices (in the case of triangles and quadrilaterals, vertices plus midpoints) are connected by straight lines, and the intersections thus formed are likewise connected. What emerges is an intricate network defining internal structures unique to that polygon. Given such a network the inquiring eye has little difficulty picking out an endlessly diminishing series of concentric title polygons and polygrams in several orientations. Only slightly less salient are various non-title regular or semi-regular forms. Figure 3.

Since our interest lies in differences of uniformity, the forms of greatest relevance are the regular forms, the ones with equal sides and angles, and with optimal symmetry. Further, since our interest lies in distinguishing among the regular polygons, it is the non-“title” forms that concern us – not the pentagons and pentagrams within a pentagon, for each regular polygon has a comparable set. Rather it is those, created by the title forms, which have another number of sides, the squares within octagons, the pentagrams within decagons, and the like. To keep things within bounds, I will consider only fully regular figures in the following study. As it turns out we have a convenient indication of which these are in each case, namely the ones figuring in the decomposition of its stellations.

Stellations are star-like forms (hence the name) produced by extending the converging sides of a polygon in both directions to points (hence they exist only where the number of sides exceeds four). The number of distinct stellations (polygrams) that can be formed from a polygon depends on how many converging sides it has. Thus the hexagram has only one, whereas an octagon has two, designated by the so-called Schäffli numbers 8/2 and 8/3, the denominator referring to the fact that the points are formed by extending sides i and i+2 or i+3. The full set of regular forms belonging to the content of a polygon is conveniently exhibited by its stellations and the forms into which they can be decomposed. And since stellations exist within the polygon as well as beyond it there is no question but that they are part of its content.

Stellations whose Schäffli number n/m reduces to an integer i decompose into m concentric, regular i -agons angled relative to each other. Thus three stellations of the dodecagon, 12/2, 12/3, and 12/4 decompose into two hexagons, three squares, and four equilateral triangles respectively. Figure 4.

Stellations whose Schäffli number reduces to a smaller fraction but not to an integer decompose into regular polygrams. The 10/4 stellation of the decagon decomposes into two pentagrams, since 10/4 reduces to 5/2. Figure5.

There is a neat arithmetic rule governing which regular non-title polygons and polygrams a polygon thus contains. In the first instance an n -sided polygon contains all the polygons whose number of sides is a factor of n, plus those polygons' associated polygrams. Thus an octagon contains a square because 4 is a factor of 8. The dodecagon, with its factors of 2, 3 and 4, contains the equilateral triangle, the square and the hexagon. However, this is not all. For in the network the multiple of the title polygon shows up fairly early, the 16-sided deca-hexagon in the octagon. If the same networking is applied to the deca-hexagon, its multiple likewise appears. And so on, endlessly. By the rule, all the polygons representing factors are contained. Since 20 is a multiple of both 4 and 5, hidden within the square is a pentagon, and vice versa. This leads finally to the conclusion that all polygons contain all others.

Still, regular polygons are sharply differentiated by layers of content. The factors of the title number are represented by forms that show up early in the networking process. Those of the first multiple are far less salient and those of subsequent multiples are deeply buried indeed. This is both an objective fact and a psychological one analogous to the situation found in musical harmony. All the overtones are present in a given tone, but the early members – octave, fifth, fourth, third, etc. – are the ones that are acoustically relevant to our experience of consonance or dissonance. So I propose that we gauge the aesthetically effective content of a polygon by those forms that show up fairly early. On this basis it seems reasonable to limit the regular-form content to the forms representing factors of the first multiple.

Returning to the stellations of the dodecagon we find one more case to consider, 12/5, which does not reduce to a simple fraction. Its non-reducibility is expressed in its form. When one follows the path of its lines from point to point one is led through the entire maze back to one's starting point. This implies that it has no decomposition via regular polygons or polygrams.

However, the 12/5 stellation decomposes into a hexagramic demi-stellation as shown in 12/5a below. Demi-stellations are fully regular forms created by extending one side only of given sides of the polygon, resulting in a star with one-half, one-third, one-quarter (etc.) the points of the source polygram. Even-sided polygons have a distinction unique to themselves connected with this: all of their integral stellations are decomposable into demi-polygrams. Figure 6 plus the 10/3a in Figure 5.

As the 12/3a and 12/4a figures show, demi-stellations also apply to polygrams whose Schäffli number reduces to an integer.

In the case of prime number polygons, no decomposition is possible in terms of fully regular forms. Thus the best resolutions of the heptagon's 7/2 and 7/3 stellations perforce resort to such forms as are used in 7/2b and 7/3b below. Figure 7.

The difference between these and fully regular figures is: (a) some sides or some angles are unequal; (b) each form possesses only minimal symmetry; and (c) the decomposition is inefficient (redundant). For instance only one of the points of the third form in 7/2b and 7/3b does any work. The same traits are present in the forms in 9/2b. Such non-regular figures are required for at least one stellation of every odd-sided polygon, even for non-primes such as the nonagon or deca-pentagon (15 sides).

The presence of more or fewer regular forms in the content of regular polygons offers a way to make sense of the idea of their having significantly different blends of uniformity and variety. But the variety in question is nothing like Hutcheson's number of sides. Rather it is diversity of regular forms, that is, a diversity of uniformities . This opens the way to a rule like Hutcheson's that favors polygons that have the same (basic) uniformity as others but score higher in diversity of uniformities .

3

Gauging differential uniformity and diversity of uniformities of regular polygons

Prompted by this revision of Hutcheson's rule, I make the following modest proposal for provisionally ranking regular polygons by their diversity of uniformities of the sort so far presented. (Other dimensions of regularity can be dealt with separately.) The ground rules for scoring are as follows. (1) Discount the “title” polygons and polygrams of the polygon in question, i.e., the pentagon and pentagram when assessing the pentagon. (2) Count all regular non-title forms (polygons, polygrams and demi-polygrams) in the polygon and its first multiple. The reason for counting those of the first multiple is that the multiple is also easily discoverable within the network of connections.7 Differences of size or orientation are not counted, but differences of angle are. (3) Compare the sum of regular non-title forms with the number of sides of the polygon (alternately, of the polygon and its multiple). 8 The highest proportion possible is somewhere around 2 n for a polygon with n sides. Accordingly we may set that as our effective perfect score, calculate the ratios on that basis, and then adjust the maximum if any score exceeds it. When the dust settles it turns out that the scores are the same regardless of whether we use the sides of the polygon or the sum of the sides of polygon and its first multiple, as the parenthetical figures attest. Figure 8.

Triangle (+ hexagon): 2 for 3. 9 .333 (.303) 2 for 9 .222 (.303)

Square (+ octagon): 4 for 4 .500 (.455) 4 for 12 .333 (.455)

Pentagon (+ decagon): 3 for 5 .300 (.272) 3 for 15 .200 (.272)

Hexagon (+ dodecagon): 11 for 6 .917 (.833) 11 for 18 .611 (.833)

Heptagon (+ deca-tetragon): 8 for 7 .571 (.520) 8 for 21 .381 (.520)

Octagon (+ deca-hexagon): 11 for 8 .688 (.625) 11 for 24 .458 (.625)

Nonagon (+ deca-octagon): 16 for 9 .888 (.808) 16 for 27 .593 (.809)

Decagon (+ icosagon): 22 for 10 1.100 (1.000) 22 for 30 .733 (1.000)

In general the scores confirm the impression previously conveyed of primes as the least various, and the factor-rich even-sided polygons as the most richly diverse, not just absolutely, which is trivial, but relative to their basic complexity (number of sides). The only surprise is that a non-prime odd-sided figure such as the nonagon ranks so high, especially in relation to the octagon. This results from its multiple being an exceptionally rich even-sided figure, the deca-octagon, whereas the multiple of the octagon is the more modestly endowed sixteen-sided deca-hexagon. The nonagon also profits from a trait common to all odd-sided figures, namely that they have one more stellation than their predecessor and the same number as their successor.

4

Regularity of n -agonic patterns within n -agons

Inspection of the diagrams reveals that it is not simply the multitude of regular forms in the content of polygons that affects its uniformity and variety, but the patterns they form, since these are also variably uniform and diverse. Coherence is immediately obvious in the suite of concentric forms. That much is common to all regular polygons. Differential coherence is evident in the decomposition of the stellations within that suite. The non-title forms so appearing are also concentric. What remains to be assessed are the patterns consisting of small-scale non-concentric iterations of the title polygon and its stellations at salient nodes within the polygon. For example an octagon's angles of 45º, 90º and 135º produce tightly ordered patterns of octagons, octagrams and squares within the parent polygon, as in the following. The first picks out a full set of 40% octagons within the larger figure. The second, B, places four 50% 8/2 octagrams in the vertices and one in the center, the third, C, centers four 50% 8/3 octagrams at the midpoint of four sides; and D overlays four 40% octagrams centered at midpoints with a dark central octagram on top (ignore the additional pattern faintly visible beneath). Note the ubiquity of squares at different size levels and orientations. Figure 9.

When we attempt to find comparable heptagonic structures in heptagons, the best we can do falls far short. Passable results are obtained only when we use a full complement of seven, as in A below. Even here the symmetry of the overlaps is a grade lower than it is in its octagonic counterpart above. And from that point on things go downhill. The best we get using three or four half-sized heptagrams are awkward or eccentric patterns such as those in B and C, a far cry from the octagonal or even the nonagonic cases. Figure 10.

It is not difficult to apply similar procedures to sets of these patterns as were found applicable to the more basic content of the polygons in Figure 8. For we can count the regular shapes within the pattern and determine the symmetry of the patterns as a whole and of the patterns within them. Thus

pattern 9A (Figure 10.1 above) has optimal symmetry (8/8 rotational, 9/9 reflective) while 9B-D have 8/3 rotational and 9/3 reflective symmetry. The latter three contrast markedly with the corresponding heptagonal patterns 8B-C in Figure 10 which have 6/0 rotational and 7/1 reflective symmetry.

Half-size outline polygonal patterns compared

It is instructive to compare the set of half-sized n -agonic outline figures placed in the vertices of their title polygons. The results tend to confirm the prior findings. Figure 11.

As the number of sides reaches ten the differences become less noticeable, but two features hold constant. The number of separate rhombuses required (indicated by the small icons) favors the even-sided patterns in respect of uniformity. The even-sided figures do more with fewer forms, hence have an easily measured access of uniformity on that account. But also, in consequence of this and the relations among the angles of their forms, they have a firmer, undistorted character than do the odd-sided figures. Also, the pattern in the center of the even-sided patterns is free of the crossovers that confuse parallelism and convergence, which is particularly conspicuous in the heptagon. This confusion creates a planar polygram that stretches uneasily across an apparent declivity. The odd-sided patterns have more diversity, but many of their diversities are diversities of low-grade uniformity.

What is evident even in these outline patterns is also so in various others, and once more there is a conspicuous difference among the polygons. None of the others comes close to the remarkable versatility of the hexagon in suggesting precise and consistent spatiality. Especially when the relevant shapes are highlighted by toning, the hexagon proves prodigious in this respect. Here is a sampling. Figure 12.

There is no puzzle about this unique capacity. It follows straightforwardly from the fact that the patterns exactly correspond to a familiar type of parallel projection of cubic forms (in the case of E some non-cubic ones too). The octagon is in distant second place.

5

Other dimensions of diversity of uniformity

Time permits only the barest mention of other dimensions.

1. Proportionality, which is applicable to forms within regular polygons. The most clamorous claimant to consideration is the celebrated golden triangle, whose sides are in golden proportionality to the base (angles 36º, 72º, 72º). Here the pentagon is the primary beneficiary: it possesses a remarkable density of golden triangles (A and B below), and this feature is inherited by its multiples: the decagon (C), the deca-pentagon, et al. Indisputably this proportionality deserves consideration; like the other forms it is ubiquitous in the figures in an infinite series of sizes, as is plain from the samples given below of the pentagon and decagon. The golden ratio is also a case of uniformity, namely the identity of ratios of sides a:b=b:(a+b). Diversity is also implicated in the difference of side length, in contrast to the perfectly uniform 1:1 ratio holding between the sides of any fully regular figure. There is reason to give the pentagon due credit for the uniform proportionality of its constituent forms, but I doubt that will bring it to the uniformity-variety level of, say, the hexagon. Figure 13.

(2) Contribution of polygons to regular and semi-regular solids. Only six polygons, the first two odd-numbered and four even-sided, form faces of the five Platonic, the thirteen Archimedean or the ninety-two Johnson solids. All fall within the set we are considering. Left out are the heptagon and nonagon.

(3) Aggregation uniformities. Three polygons aggregate densely: the equilateral triangle, the square and the hexagon. Others leave spaces, some regular and some non-regular. Figures 14 (i-ii).

(4) Polygonal-polygonal circumscription and inscription. All regular polygons circumscribe and are circumscribed by circles, but only some do this for other regular polygons. Figure 15.

7

Taking stock of the data

The overall outcome, as I see it, is that there are several viable, partial measures of the differences of uniformity and variety among the regular polygons. These tend to agree in a general way, but also have interesting differences. It is important not to overlook the variations in capacity as one moves from category to category. The comparatively low-scoring heptagon, for example, has some quite creditable patterns, even if they have a certain flavor of the eccentric. Several examples are given in Figure 18 in the appendix at the end of the endnotes. And of course the beauty of polygonal regularity is by no means the only species of beauty that is represented by these forms. As an example of the strangely fascinating patterns that emerges from a close study, I give you the half-sized 9/4 nonagram pattern, in outline and then with each nonagram toned 30%. Amid their rigorous regularity, these figures have, to me, a hilarious eccentricity. Figure 17 .

An obvious question which I cannot presently answer (one of many) is whether the partial measures can be combined into an overall measure that is both sharp and credible.

And beauty?

Even if clear, complex, relations of uniformity and variety (diversity of uniformity) can be established separating the regular polygons into a credible ranking (not excluding many on the same level) will that justify ascribing more beauty to those of higher rank? The main argument for the affirmative, in my view, rests largely on such things as the manifest aesthetic deficiencies of the non-regular forms required for the best decomposition of prime number stellations, such as the heptagrams, as shown in Figure 7, and the best patterns of fractional heptagons and heptagrams in Figure 10, compared with the merits of their counterparts in higher ranked polygons, e.g. the dodecagon and octagon. The beauty of regularity is not by any means the only species of that hugely polyspecific value. But it is not an inconsiderable species, and it is what Hutcheson and the others have in view when they assess polygons, little as they were able to analyze it. I invite skeptics to study the full range of diagrams (only very partially displayed on the handout) and test their aesthetic responsiveness against mine. I think we will find our responses converging. 10

8

Uniformity and Variety psychologically considered. At long last I come to the psychological criterion, to which only passing references have been made. All of the philosophers agree that our beauty-response is inhibited by extremes of uniformity and variety, even though they do not agree as to where the threshold falls. I think we may discern two factors in their conception, saliency and intelligibility.

1. The saliency factor

A figure is salient when it stands out from, is easy to pick out of, a context. This is true of the pentagrams resident within the web of connections in the regular pentagon. There are countless shapes that are not salient in the web.

Stressing the initially non-salient forms sets up conflict with the initially salient ones, as in A-D below, which it is safe to say are not nearly as beautiful as the patterns in A-C above.

A figure is saliently this or that when the property in question is easy to pick out from other properties. Thus a very slightly skewed but otherwise regular quadrilateral is not salient in shape, since it approaches so close to the square that it creates uncertainty whether it is a square or only an approximation thereto. This may relate to uncertainty about whether one's point of view explains the appearance, or to ambivalence about whether to read the shape in depth, or to difficulty in drawing (or shaping) such a slight difference.

2. The intelligibility factor

A figure is intelligible to the extent that we have ready ways of grasping its properties. Slight deviations from regularity, even when visually detected, create discomfort because they produce difficulties in measurement, of area, of length of the irregular side that cannot be lined up with the others end to end. No technology, including drafting images on paper in geometrical studies could easily adapt to the indefinitely numerous “arbitrary” lengths and angles. Carpentry, surveying, and other basic technologies deeply reflect our cognitive system's capacity to cope with shapes.

9

Finally, and yet more sketchily, just a few ideas as to how we can integrate or if not integrate then arbitrate between the two criteria so far is beauty is concerned. The philosophers shuttle back and forth between the two, which is not theoretically acceptable. I believe we can resolve the tension in a way that should be acceptable to them. The result is a qualified response-dependent theory of beauty heavily hedged by optimizing conditions. Tension is resolved by distinguishing between qualities that are beautifully suitable to our cognitive faculties and qualities that are beautifully suitable to more potent cognitive faculties that we can clearly conceive. Implementing this general idea requires much work on the concept of suitability, which of course I am in no position to do at present. I can only indicate some possible consequences.

Kames, for instance, puts heavy stress on what he calls a moderate movement of the flow of ideas. On this basis the uniformity of the circle, as of the square's parallel sides, makes these figures more beautiful than the equilateral triangle, whose inclining sides are “obscure,” because these features make the circle and square easier to take in in a single act of moderate effort. 11This is apt to strike us as too timid a conception of an ideal state of cognition. Hutcheson has a distinctly more vigorous sense of human good. For him, apparently (and plausibly), there are more vigorous sustainable states of cognitive processing, and these flourish best when we deal with more complex forms, or in enriching simple forms with expressive or symbolic content.

We can also distinguish between species of beauty: beautiful perceptual legibility as opposed to a beautiful intricate complexity that yields its secrets only to the most discerning, that is, to searching examination by the most persistent and indefatigable devotees. Arguably even incomprehensible beauties should not be excluded a priori as long as the failure is due to the limitations of our systems; nor should high, hard, daunting beauties,or austere or formidable beauties. Not all beauties need be smiling, comfortable, gracious.

We can extrapolate from what we can handle to what we could handle if our faculties were less frail. Doing so need not take us beyond the sense of beauty. Our sense of beauty does not have to be omnipotent in order for beauty to be response-dependent any more than our color-sense need be the last word on color for color to be response-dependent.

Endnotes

1. As I conceive it, beauty in a sense of beauty scheme is the disposition of the object to elicit a favorable – i.e. pleased – reponse from the viewer's awareness of such properties as uniformity amidst variety. The latter are the properties in which the pleasure (typically qualified as disinterested) is taken.

2. Perhaps we could call the general relation one of visual congeniality (to our faculties).

3. Note that the beauty I mean to deal with is neither purely visual nor purely conceptual beauty. Both aspects of cognition are involved. Also it is what Kames called intrinsic and Hutcheson absolute or original beauty, as opposed to the beauty of suitability to a function or of representation or expression. The latter were referred to as relative beauty.

4. Uniformity of parts in these geometrical cases is unlike similarity in that two sides or angles are uniform only if they are exactly similar. Greater and lesser degrees of uniformity apply only to sets of parts or wholes collectively.

5. Paradigm cases of correspondent parts are opposite elements in plane figures (lines or angles), functionally coordinated parts of organisms (limbs, eyes, ears), matching parts of constructions, mechanisms, buildings, or of natural phenomena generally. “Parts” may also refer to opposing sides or halves of things -- hills or animal bodies. Such correspondences already imply a measure of uniformity, since many irregularly shaped objects do not have clearly correspondent parts. Defining uniformity as Gerard does is subject to the objection that it fails to cover cases where a graphic element, such as line, color, or texture, is uniform in character independently of correspondences. These forms of uniformity can be included by broadening the notion of to cover similarities among correspondent or adjacent parts, segments or areas . The broadened criterion admits such figures as A and B as examples of uniformity of line, C and D as examples of uniformity of tone and texture, independently of any clearly correspondent parts or segments:

Lines can of course be more or less uniformly smooth, hard or soft edged, jagged, constant or evenly graduated in weight, etc.; colors and textures can be variously uniform or variegated within areas -- all without any of these being correspondent.

6. Regular figures have as many axes of reflection as they have sides. The square has four, the decagon 10, and so forth. The same is true for angles of rotation, but In scoring basic regularity below, I count n-1 angles of reflection, since there are only that many transformations by rotation. One might think that polygons with more sides are due a higher grade of symmetry. I think it is better to rate a polygon's symmetry score by how close it comes to the maximum for its number of sides. On this basis all regular polygons, polygrams and demi-polygrams are maximally symmetrical. There are more substantial ways in which the number of sides affects the uniformity and variety of regular polygons.

7. The forms contained by polygons come to light early or late as the network of connections is constructed. The first multiple shows up early, the later ones significantly later, and correspondingly the first multiple more significantly affects our experience. The situation is similar to that of musical harmonies, where the early members of the overtone series determine what we experience as consonance and dissonance. The full series contains all the tones, just as the full series of forms in a polygon contains all regular forms. In analogy with the harmonic situation, it is reasonable to take the effective content of a polygon to be what appears at an early level. Accordingly I suggest we take it as embracing the regular polygons and polygrams of the stellation-decomposition of it and its first multiple, but excluding the forms found only in its further multiples. I believe this suffices to explain the chief differences in our experience of the polygons.

8. If we do not count the contribution of the multiple the results are:

Triangle: 1 for 3 (?) [.333]

Square: 1 for 4 (?) [.250]

Pentagon: 0 for 5 .000

Hexagon: 1 for 6 .166

Heptagon: 0 for 7 .000

Octagon: 2 for 8 .250

Nonagon: 2 for 9 .222

Decagon: 3 for 10 .333

These scores do not seem to me to reflect the importance of the variety of uniformities in the figures.

9. Arguably we should count the trigrams discoverable within the triangle, even though they are neither stellations nor demi-stellations of it or of the hexagon. Adding them would bring the triangle to the 3 for 3/ 3 for 9 level. Here is an image (A) showing two trigrams readily discovered in the equilateral triangle. By the same token, however, adding them would push us to search other other regular forms of a similar sort. For instance there are pentagrams within the pentagon with fractions of the 36º angle in the 5/2 stellation as in B.

10. Inured as we now are to difficult visual art, that is, art whose visual order is cryptic or minimal, we are apt to find examples like the heptagonal ones more interesting than the more richly regular octagonal ones. But this, in my opinion, does not show that the latter do not stand higher in the species of beauty which they centrally represent. It only makes them less beautifully suitable to a certain kind of visual address, namely one that looks for difficult beauties. This interesting topic deserves much more attention than I can give it here.

11. It may be an empirical fact that we have more trouble telling whether a triangle is equilateral than we have telling whether a square is. However, this is doubtful, since we commonly overestimate the vertical dimension, tending to make our squares slightly too squat. Nonetheless it is probably true that we feel more secure in judging squarishness than equilateral triangularity. And this may well be what Kames is guided by.

Appendix. The figure below appeared on the handout testifying to the remarkable kaleidoscopic power of the regular polygon to create order from arbitrarily selected forms within its network when the polygon as a whole is rotated in accordance with its angles of rotational symmetry and the selected form is iterated at each angle.

Figure 17

Figure 18: Heptagonal patterns of creditable uniformity and diversity

References

Rudolf Arnheim 1966. Art and Visual Perception: a psychology of the creative eye. Berkeley, California: University of California Press.

Monroe Beardsley, 1958. Aesthetics: problems in the philosophy of criticism. New York: Harcourt, Brace and World.

Alexander Gerard, 1759. An Essay on Taste together with observations concerning the imitative nature of poetry. A facsimile reproduction of the third edition (1780) with an introduction by Walter J. Hipple, Jr. Gainsville Florida: Scholars Facsimiles and Reprints, 1963.

Walter John Hipple, Jr. 1957. The Beautiful, The Sublime, and The Picturesque in Eighteenth Century British Aesthetic Theory. Carbondale, Ill.: The Southern Illinois University Press.

Alan Holden and Phylis Morrison, 1892. Crystals and Crystal Growing. Introduction by Philip Morrison. Cambridge, Mass.: The MIT Press.

Henry Home, Lord Kames, 1763. Elements of Criticism, 6th Edition (1785). Edited and with an introduction by Peter Jones. Indianapolis, Ind.: Liberty Fund. 2005.

H. E. Huntley, 1982. The Divine Proportion: a study in mathematical beauty. New York: Dover Publications.

Francis Hutcheson ,1726. An Inquiry into the Original of Our Ideas of Beauty and Virtue in Two Treatises. Edited and with an introduction by Wolfgang Leidhold. Indianapolis: Liberty Fund, 2004.