1
PHIL 332 Philosophy of Beauty -- Core Text, Part two
Two key Platonic passages about beauty as a Form
(a) Phaedrus 247C-251A
After the rather technical summary of Plato's idea of beauty as an abstract Form, it may come as a welcome change of pace and tone to encounter the chief passages in his writings where beauty holds center stage. The first of these is the dialogue Phaedrus, the nominal topic of which is rhetoric. The speeches under discussion are about love, or in the Greek fashion about Love, which was regarded as a divine force. Socrates, Plato's spokesman, invents a grandiose myth in which the highest type of love is represented as inspired madness which drives souls on earth, and even moreso in heaven between earthly lives, toward knowledge of the highest realities, among which is the Form of Beauty. In the excerpt given here the souls are in their disembodied state prior to rebirth on earth. The reasoning part of each soul drives a chariot through the sky pulled by a white and a black horse (allegorically, souls are impelled by their desires, good and bad). With great effort they strive to follow the immortal gods "to the top of the vault of heaven" from which vantage point can be glimpsed a "heaven which is above the heavens". This is the realm of the Forms. (trans. B. Jowett)
There abides the very being with which true knowledge is concerned: a reality which is colorless, formless, intangible, visible only to mind, the pilot of the soul ... she beholds justice and temperance and gains knowledge absolute, not that which is found, in varying forms in one or other of those regions of becoming (1,2) which we men call real, but real knowledge really present where true being is. (247C-D)
[1. He means a priori knowledge, on which ahead, section 9. 2. Region of becoming = world of growth and decay. He means the world of space and time.]
The gods can mount high enough to see all this steadily, but any lesser soul's view is more or less imperfect, intermittent and distant; and when a soul is again embodied the person it becomes has a correspondingly variable, but always imperfect recollection of the Forms:
the soul which has seen most of truth shall be placed in the seed from which a philosopher or lover of beauty and follower of the Muses (3) will spring; that which has seen truth in the second degree shall be some righteous king or warrior chief; the soul which is of the third rank shall be a politician, or business manager or trader; the fourth shall be a lover of gymnastic toils, or a physician; the fifth shall lead the life of a prophet or seer; to the sixth the character of a poet or some other imitative (4) artist will be assigned; to the seventh the life of an artisan or husbandman; to the eighth that of a sophist or demagogue; to the ninth that of a tyrant; -- all these lives are states of probation, in which he who does righteously improves, and he who does unrighteously deteriorates, his lot. (248C-D)
[3. The Muses were patron deities of the verbal arts and their associated arts of music and dance. Philosophy, in the wide sense of love of wisdom, was one of the verbal arts. But Plato here takes the Muses as patrons only of such word-art as is suitable for real divinities. 4. "Imitative" poetry is here considered beneath the Muses, as indicated by the low rank Plato assigns it. ]
2
The higher sort of person, Socrates continues,
When he sees any earthly beauty is transported with the recollection of the true beauty; he would like to fly away but he cannot; he is like a bird fluttering and looking upward and careless of the world below; and he is therefore thought to be mad. And I have shown this of all inspirations to be the noblest and highest and the offspring of the highest; that it is recognized to be such by him who has or shares in it; and that he who loves the beautiful is called a lover because he partakes of it. For, as has been already said, every soul of man has in the way of nature beheld the true being; this was the condition of her passing into the form of man. But all souls do not easily recall the things of the other world; they may have seen them for a short time only, or they may have been unfortunate in their earthly lot, and, having had their hearts turned to unrighteousness through some corrupting influence, they may have lost the memory of the holy things which once they saw. Only a few retain an adequate remembrance of them; and they, when they behold here any image of that other world, are rapt with amazement; but they are ignorant of what this rapture means, because they do not clearly perceive it for what it is. For there is no radiance (5) in our earthly copies of justice or temperance or those other things which are precious to souls: they are seen through a glass dimly; and there are few who, going to the images, behold in them the realities, and these do it only with difficulty. But beauty could be seen, brightly shining, by all who were of that happy band, -- we philosophers following in the train of Zeus, others in company with other gods; at which time we beheld the beatific vision and were initiated into a mystery (6) which may be truly called most blessed, celebrated by us in our state of innocence, before we had any experience of evils to come, when we were admitted to the sight of apparitions innocent and simple and calm and happy, which we beheld shining in pure light, pure ourselves and not yet enshrined in that living tomb which we carry about now that we are imprisoned in the body like an oyster in his shell. Let me linger over the memory of scenes which have passed away.
[5. no radiance: none compared with that of the Forms, though plenty of radiance compared with the dullness of unbeautiful things, as is evident from the next paragraph. 6. initiated into a mystery refers to initiation rituals in ancient mystery religions, the revealed truths of which were forbidden for an initiate to disclose to anyone else.]
But of beauty, I repeat that we saw her there shining in company with the other celestial Forms; and coming to earth we find her here too, shining in clearness through the clearest aperture of sense. For sight is the most piercing of our bodily senses (7); though not by that is wisdom seen -- her loveliness would have been transporting if there had been a visible image of her, and the other ideas (8), if they had visible counterparts, would be equally lovely. But this is the privilege of beauty, that being the loveliest she is also the most palpable to sight.
[7. most piercing of our bodily senses: in what specific ways is sight superior to hearing or touch? Can you think of any way in which sight is inherently superior to the other senses -- one that is not merely the result of our having been better trained to use it? 8. the other ideas: esp. truth, goodness, justice, etc.]
3
Now he who is not newly initiated or who has become corrupted, does not easily rise out of this world to the sight of true beauty in the other, when he contemplates her earthly namesake; instead of being awed at the sight of her, he is given over to pleasure, and like a brutish beast rushes on to enjoy and beget; he consorts with wantonness and is not afraid or ashamed of pursuing pleasure in violation of nature (9). But he whose initiation is recent, and who has been the spectator of many glories in the other world, is amazed when he sees anyone having a godlike face or form, which is the expression of divine beauty... (249D-251A)
[9. violation of nature: At the extreme, incest, bestiality, cannibalism, and so forth; less radical cases are adultery, cruelty to parents, neglect of children, etc.]
Commentary
Myth such as this is partly allegorical and partly literal. It is reasonable
to take it as asserting Plato's belief in reincarnation and in souls existing
disembodied between lives on earth. Also, his belief that disembodied souls
are able to operate at a higher intellectual level than can their embodied counterparts.
Those parts of the myth are to be taken literally. But much of the rest is allegory.
One cannot see the Forms with one's eyes, and disembodied souls don't have eyes
anyway. Their "sight" of the Forms is a purely intellectual comprehension
of them, a conceiving rather than perceiving. But seeing is a natural metaphor
for this because the superior insight of the disembodied souls has the vivacity
of perception -- it is that full and sharp.
Further, we don't have to believe Plato's story about reincarnation to derive some insight from it about our knowledge of the Forms. In particular we needn't take our learning to be literally a process of recollection. For us recollection can function as a metaphor for the sudden dawning upon us of the truth about something, as when we suddenly see why a mathematical proof is valid. Or when we figure something out by ourselves, without being told. The insight just comes out of the blue, like a name we have been trying to remember. The mind clicks, just as the memory does.
The Forms' otherworldy existence, in a heaven beyond the sky, is similarly allegory for their abstract and substantial nature. Abstract "existence" is non-spatial and non-temporal, hence elsewhere than in our world (but only in a manner of speaking, since strictly speaking abstract things can't be anywhere -- the concept of location doesn't apply). Further they are "substances", in a philosophical sense. They exist in their own right, the way we think of ordinary objects existing. A substance contrasts with its passing states or relations, as a table is thought to contrast with its states (being wet from rain) or relations (being sat on by Fred). It is the relatively permanent "subject" we detect beneath or within the variable surface appearances. That is why Plato can describe the abstract Forms allegorically as if they were visible objects.
4
All the preceding is about Forms in general. What about beauty in particular? What does the passage tell us about it?
First it says that Beauty, the Form, is the most beautiful of all the Forms. All the Forms are beautiful but it is the "loveliest". Beauty is also "the most palpable to sight", which in this context means eyesight, not the intellectual vision of disembodied souls. Other Forms, justice and wisdom and all the others, never present themselves so fully in visible form. This visual connection is reinforced by Plato's metaphors of light: the Forms are "beheld shining in pure light" in the other world, and some of that radiance survives in the case of Beauty even on earth.
Sight is "the most piercing of our bodily senses" yet hearing seems also to share the ability to appreciate beauty. For musical beauty is elsewhere fully acknowledged by Plato. To a lesser extent smell and also taste have this capacity. So we can speak more generally of the sensory connection of beauty. This sets it apart from the other Forms, even from those which are very beautiful.
Beauty is also said to have a special connection with love. It is the ultimate object of all love. To love is to love the beautiful, or as we might put it, to love the beautiful in whatever one loves. To love a person is to love what is beautiful in, or about, that person. The connection with love also brings in the connection with pleasure, since to love a thing is to take joy in it
These leads help set beauty off from the other Forms, which is essential if Beauty is to be more than a word. They do not, however, give us a definition or tell us much about what Beauty is.
The next excerpt adds some further leads.
(b) Symposium 209D-212A, trans. Benjamin Jowett.
This famous passage on the ascent of the soul to a vision of true beauty occurs in the dialogue Symposium (or Banquet), when Socrates is regaling his fellow diners with the story of his instruction in the art of love by the priestess Diotoma of Mantinea. She has explained that love is properly personified not as a mighty god but as a demi-god whose nature is restlessly to seek for what he does not yet possess. She has also set Socrates straight about sexual love, which according to her is not simply love of the beautiful, but mainly thirst for personal immortality achieved vicariously through one's progeny. Then, in the excerpt given below, she spreads before him the whole spectrum of love reaching from the commonplace to the exalted. Beyond the physical lie the intellectual forms of love, the intellectual love of beautiful systems of law, morality and science which promote the advancement of culture. And finally, above even these there is a final, rapturous vision of the highest object of love, Beauty Itself. To become aware of it is to enter into the higher mysteries of love. (Diotoma speaks as a priestess of a mystery religion into which people were initiated by ceremonies which divulged secrets about the divine, especially about the afterlife).
5
These are the lesser mysteries of love, into which even you, Socrates, may enter; to the greater and more hidden ones which are the crown of these, and to which, if you pursue them in a right spirit, they will lead, I know not whether you will be able to attain. But I will do my utmost to inform you, and do you follow if you can. For he who would proceed aright in this matter should begin in youth to seek the company of corporeal beauty; and first, if he be guided by his instructor aright, to love one beautiful body only -- out of that he should create fair thoughts; and soon he will of himself perceive that the beauty of one body is akin to the beauty of another and then if beauty of form in general is his pursuit, how foolish would he be not to recognize that the beauty in every body is one and the same! 2 And when he perceives this he will abate his violent love of the one, which he will deem a small thing and will become a steadfast lover of all beautiful bodies. In the next stage he will consider that the beauty of the soul is more precious than the beauty of the outward form; so that if a young person with a virtuous soul have but a little comeliness, he will be content to love and attend upon him, and will search out and bring to birth thoughts which may improve him; until he is compelled next to contemplate and see the beauty in institutions and laws, and to understand that the beauty of them all is of one family, and that personal beauty is a trifle. After institutions his guide will lead him on to the sciences (l), in order that, beholding the wide region already occupied by beauty, he may cease to be like a servant in love with one beauty only, that of a particular youth or man or institution, himself a slave mean and narrowminded; but drawing towards and contemplating the vast sea of beauty, he will create many fair and noble thoughts and discourses in boundless love of wisdom, until on that shore he grows and waxes strong, and at last the vision is revealed to him of a single science (l), which is the science of beauty everywhere. To this I will proceed; please give me your very best attention.
[1. By "science" is meant any organized body of knowledge (from the Latin verb to know). The science of beauty will be what I have called theory of beauty plus all its applications to particular cases. 2. Socrates does not mean that all bodies are equally beautiful, but only that beauty is a single property that exists in various degrees.]]
He who has been instructed thus far in the things of love, and who has learned to see the beautiful in due order and succession, when he comes toward the end will suddenly perceive (2) a nature of wondrous beauty (and this, Socrates, is the final goal of all our former toils) -- a nature which in the first place is everlasting, knowing not birth or death, growth or decay; secondly, not fair from one point of view and foul from another, or at one time or in one relation or at one place fair, at another time or in another relation or at another place foul, as if fair to some and foul to others, or in the likeness of a face or hands or any other part of the bodily frame, or in any form of speech or knowledge, or existing in any individual being, as for example, in a living creature, whether in heaven or on earth or anywhere else; but beauty absolute, separate, simple, and everlasting, which is imparted to the ever growing and perishing beauties of all other beautiful things without itself suffering diminution or increase or any change. He who, ascending from these earthly things under the influence of true love, begins to perceive that beauty, is not far from the end. And the true order of going, or being led by another, to the things of love, is to begin from the beauties of earth and mount upwards for the sake of that other beauty, using these as steps only, and from one going on to two, and from two to all fair bodily forms, and from fair bodily forms to fair practices, and from fair practices to fair sciences, until from fair sciences he arrives at the science of which I have spoken, the science which has no other object than absolute beauty, and at last knows that which is beautiful by itself alone.
[3. Here "perceive" = grasp conceptually, not see, hear, touch, etc. Note the criteria of aesthetic excellence mentioned here, namely, (a) everlastingness, (b) changelessness, (c) purity, (d) action/state invariance (that is, not beautiful only when, say, running not walking, swimming not wading, cheerful not sad, etc.), (e) context-invariance, (f) immunity to perspectival distortions, (g) abstractness. Please note that (a)-(g) set the forms above concrete particulars and to an extent help rank concrete particulars relative to each other; but they do not serve to rank Forms relative to each other. Hence they do not exhaust Plato's criteria of aesthetic excellence.]
6
This, my dear Socrates,...is that life above all others which man should live, in the contemplation of beauty absolute; a beauty which, once beheld, would be seen not to be inferior to gold and garments and pretty boys (4), whose presence now entrances you -- you and many others would be content to live seeing them only and conversing with them without meat or drink, if that were possible; you only want to look at them and to be with them. But what if man had eyes to see the true beauty -- the divine beauty, I mean, pure and clear and unalloyed, not infected with the pollutions of the flesh and all the colors and vanities of mortal life -- thither looking, and holding converse with the true beauty simple and divine? Remember how in that communion only, beholding beauty with that by which it can be beheld, he will be enabled to bring forth not images of beauty but realities (5) (for he has hold not of an image but of a reality), and bringing forth and nourishing true virtue will properly become the friend of God and be immortal, if mortal man may. Would that be an ignoble life? (209D-212A)
[4. "Pretty boys" because Socrates is speaking of the homosexual love by an adult of an adolescent boy, which many ancient Greek intellectuals considered finer than heterosexual love. 5. "Realities" here refers to virtuous deeds or political achievements or the products of educational successes, etc. These are beautiful realities rather than the fictive "imitations" of them found in art and literature.]
Commentary
The natural order of progress in love has two sides. On the one hand it implies variable difficulty in appreciating different types of beauty. Sensible beauties are easier to perceive and love than are intellectual ones. On the other hand it implies a hierarchy of beauty, since the easier beauties do not stand as high as the harder ones. As one advances up the ranks one's taste does not merely become wider. It gets better. So we have here a rough ranking of beauty on the continuum discussed earlier. Plato is telling us something about his normative aesthetics.
In general, on Plato's scheme, sensible beauties are less beautiful than the ones which cannot be literally sensed (seen, heard, smelled, etc.). And abstract objects are more beautiful than concrete particulars. Finally, Beauty is more beautiful than any other Form.
Further, his picture gives some clues as to what makes some things more beautiful than others -- i.e. we are told of some beauty-making properties. In speaking of the eminence of Beauty itself Diotima stresses its difference from concrete particulars. Beauty itself is (a) eternal, (b) changeless, (c) pure (unmixed with ugliness, presumably, hence beautiful in all respects), (d) invariant across actions or states, (e) invariant across contexts, (f) unaffected by point of view (nonperspectivally beautiful, hence beautiful from every perspective, (g) beautifully intelligible, clear, well-ordered, rational, though not easy for beginners to grasp.
7
These claims are made for the highest beauty, Beauty itself, but they also
have an application to lesser beauties -- to other Forms and even to concrete
particulars. If Beauty is one and the same property in all its appearances,
some general application (at times by analogy) must be proper. And the other
things Plato says about lesser beauties tend to support generalizing (a)-(g)
into universal criteria of beauty (for Plato, that is). Of course these other
things will satisfy conditions (a)-(g) less fully. For instance, the beauty
of concrete particulars is always mixed with ugliness or at least mediocrity
even when the beauties the object has are comparatively copious and enduring. As many have noted, skin
which is beautiful seen by the normal human eye from the usual distance is not
beautiful under magnification. The most beautiful face can be contorted into
an unbeautiful expression, the finest picture may look sickly under an unfriendly
light, and so forth. (On the other hand, we must wonder whether Diotima can
be right about some of those criteria -- why should changelessness by itself
be beauty-making? Changelessness doesn't improve ugly things!)
One may wonder why I do not add holiness or divinity as a criterion for the
highest beauty. For Diotima speaks of Beauty itself as a divine thing. But divinity
is not an independent property. Rather it is defined in terms of superlative
degrees of excellence, for example in regard to properties like (a)-(g). To
be divine is merely to have the best properties to a superlative degree. So
speaking of beauty as divine doesn't add anything new, unless perhaps it suggests
that the beings with the greatest excellences, the gods, will both be beautiful
and be most at home with beauty -- know it most intimately, love and admire
it most fully, and so forth.
4. Plato's theory of beauty: selected topics
Here I collect various scattered passages in Plato's dialogues by topic, embedding them in commentary to bring out their meaning.
(a) Can Beauty be defined?
Taking "definition" in the standard logical sense of a strict equivalence of meaning, a term is definable if it is synonymous with a phrase which elucidates its meaning. Typically the explanatory phrase contains a number of terms. Thus "triangle" is definable as "three-sided plane figure". Language is built up from primitive or undefined terms by means of definitions. The primitive terms are not definable but can be taught either by ostension, that is, by showing samples of things to which the term applies, as with colors, sounds, feelings; or else by way of the axiomatic statements in which they figure, as in the case of geometrical and mathematical primitives like "point", "zero", etc.
Putting all this in terms of concepts, a concept is definable if it can be shown to be built up out of other concepts, as the concept of bachelor is built up out of the concepts of being male, being unmarried, and being marriageable. Some concepts are not complex in this way, and are not definable but are learned some other way.
In terms of Forms, we get the following: a Form is definable if it can be shown to consist of several Forms combined or "blended". The definition says how the constituent Forms are combined. Some Forms are "atomic" and cannot therefore be defined. They must be grasped in some other way than by discerning their constituents.
8
However one puts the definition question, a survey of Plato's writings on beauty turns up no strict definition, or even a clear answer to the question whether he thought beauty is definable.In one dialogue, Hippias Major 292, Socrates is shown searching for a definition. He says:
are you not able to remember that I asked for the absolute beautiful, by which everything to which it is added has the property of being beautiful, both stick and stone and man and god and every acquisition of knowledge? For what I am asking is this, man: what is absolute beauty?
The most important proposals for defining beauty in the dialogue are beauty = the useful in producing the beneficial, and beauty = the pleasant which comes through sight and hearing. The argument is intricate, unsystematic and inconclusive. Socrates gets ensnarled in problems and it is not clear whether Plato even thinks a definition is achievable.
From other passages we can glean hints as to plausible elements of a definition,
presuming a definition is possible. That is, hints as to properties so closely
associated with beauty in Plato's thought as to be likely candidates. Here are
passages that mention two such properties, which are also of interest for other
reasons.
(b) Beauty and order, measure, proportion, etc.
Order, measure, proportion, simplicity, rationality: these are constant themes in Plato's aesthetics. So any definition of beauty would have to produce the result that things strong in these properties are beautiful, other things. being equal. For example, Plato praises music which is regular over music which even though sweet-sounding and productive of a pure pleasure is "irregular". Such irregular music, he says, "is always made ten thousand times better by attaining to law and order" even though it seems "cold and displeasing" to those badly brought up. (Laws VII 802B-C) In the Philebus Socrates compares music unfavorably to the more exact "arts" (that is, skilled practices), including ship- and house-building:
Then now let us divide the arts [skilled practices] of which we were speaking into two kinds, --the arts which, like music, are less exact in their results, and those which, like carpentering, are more exact ... Of the latter class, the most exact of all are those which we just now spoke of as primary ... arithmetic, mensuration, and weighing and measuring...I mean to say, that if arithmetic, mensuration and weighing be taken away from any art, that which remains will not be much ... The rest will be only conjecture, and the better use of the senses which is given by experience and practice, with the help of a certain power of guessing, which is commonly called art [skill], and is perfected by attention and pains ... Music, for instance, is full of this...; for sounds are harmonized, not by measurement, but by skillful conjecture; the music of the flute is always trying to guess the pitch of each vibrating note, and is therefore mixed up with much that is doubtful and has little which is certain ... The art of the builder, on the other hand, which uses a number of measures and instruments, attains by their help to a greater degree of accuracy than the other arts ... In shipbuilding and house-building, and in other branches of the art of carpentering, the builder has his rule, lathe, compass, line, and a most ingenious machine for straightening wood ...(55E-56C, arranged)
9
Such stress on measurability and proportionality is deeply rooted in Greek culture, as will be shown in the section on architecture and the golden section. If beauty is definable some general concept on order of this sort must be part of the definition. If it is not definable, mathematical order must at least be a potent criterion of beauty, on Plato's view. In this he was at one with artists who like Polyclitus incorporated systems of proportions into their work. Polyclitus, a late 5th century Greek sculptor, is said to have written a book setting forth ideal human proportions and to have sculpted a statue called the Canon (rule) because it exhibited these relationships at least as far as a physical particular can.
(c) The unity (or unitariness) of beauty
One certain consequence of the sometimes obscure things Plato says about the Form of Beauty is that it is one, not many. I believe this has a clear consequence: Plato is saying that all beauties can be ranked on a single scale of comparison. Things may be beautiful for many reasons but if beauty is unitary then no two beauties are incomparable. It will always in principle be possible to say whether the one is more or less beautiful than, or equal in beauty to, the other. And if this is possible for every pair of things, then there is a single master rank-order of them in respect of their overall beauty.
This is a radical thesis, judged in terms of its consequences. But one can also see its appeal. If there is a single word beauty, as there is, mustn't there be a single property corresponding to it? And if there is, why wouldn't everything which has more or less of that property be comparable, each to each? In any case Plato's account of the ascent of the soul in the Symposium seems to commit him to the thesis. As the soul grows in appreciation of beauty it passes successively into higher realms, which are clearly regarded as being more beautiful than the lower ones. In the upper section, in the stratosphere of beauty, are the perfect Forms, and at the very pinnacle, the most beautiful of all, is the Form of Beauty itself.
In the other direction one descends from commonplace beauties of soul to those of body -- that takes us to Diotima's starting point-and presumably thence to the non-beautiful, which becomes increasingly ugly as one descends. Given the comprehensive notion of the field of beauty entertained by Diotima, it seems likely that everything belongs somewhere on this scale (more exactly, in this rank-order), that is, beauty is taken to be what was later called a "transcendental," a category which applies to everything positively or negatively. On this theory beauty is a "universal" in the strong sense of the term. As such it contrasts with those concepts which are limited to a given category of thing. For example expensiveness, or exchange value, which applies positively or negatively only to purchasables, which are far from the universal class. Thus the square root of 2 cannot sensibly said to be expensive or inexpensive, or priceless, or free. But it is not clear that anything escapes the reach of beauty.
To appreciate how daring Plato's idea of the unitariness of beauty is, we need only recognize that practically no one would claim nowadays that all beautiful things are in any sense comparable, that is, could be compared with each other in respect of beauty. By what criterion could one judge whether a string quartet is more or less beautiful than the Parthenon? Or a mathematical proof more beautiful than a mobile by Calder, say the big one hanging in the East wing of the National Gallery? Or an idyllic landscape (a real one) and a perfect physique? The things seem to differ too much, in fundamental ways, for comparisons to be meaningful. Our most confident judgments are always of things in the same or nearly the same class (medium, genre, period, type). Confidence, and especially confident precision, diminishes rapidly as the things in question are of widely different sorts. No one wants to be a judge in a universal beauty-contest.
10
Another way to present the thesis that beauty is unitary is this: however various the aspects of beauty or ugliness of things may be-and Plato certainly recognizes that they will be extremely diverse- there must always be some way to sum them up (the plusses and minuses) and arrive at a net comparative worth. If all beauties are comparable, so must be all the respects in which a thing is beautiful or ugly. Comparative deficits and merits must be able to be combined so as to yield a final, overall rank order. A beautiful mind must be capable of compensating for an ugly body to a determinable degree, so that we can rank things which differ in just these two respects. But commonly we regard such summative calculations as frivolous.
(d) Beauty and virtue
While less intrinsic an aspect of beauty than proportionality or unitariness, the connection between beauty and virtue (moral and intellectual, but let's concentrate on moral for the moment) is strong on Plato's view. He speaks of the connection mostly in terms of beauty having a good effect on the soul. Regarded that way the relation seems external to beauty, not part of its essence. But the causal effect results, in Plato's opinion, from the beautiful thing having a natural likeness to virtue, and that is an internal property. Thus in the Laws II, 650D, the music of the Egyptians is praised for keeping unchanged for centuries "melodies which have a natural truth and correctness", the effect of which is to make their youth "habituated to forms and strains of virtue." It seems that the melodies themselves are (as it were) noble, temperate, reasonable and in other ways virtuous or virtue-resemblant. So also in the Republic III, 401C-402A, Socrates insists that the current disorderly state of affairs in Greek arts must be rectified in his projected ideal state:
Let us rather search for artists who are gifted to discern the true nature of the beautiful and graceful; then will our youth swell in a land of health, amid fair sights and sounds, and receive the good in everything; and beauty, the effluence of fair works, shall flow into the eye and ear, like a health-giving breeze from a purer region, and insensibly draw the soul from earliest years into the likeness and sympathy with the beauty of reason
And therefore, I said, Glaucon, musical training is a more potent instrument than any other, because rhythm and harmony find their way into the inward places of the soul, on which they mightily fasten, imparting grace, and making the soul of him who is rightly educated graceful, or of him who is ill-educated ungraceful; and also because he who has received this true education of the inner being will most shrewdly perceive omissions or faults in art and nature, and with a true taste, while he praises and rejoices over and receives into his soul the good, and becomes noble and good, he will justly blame and hate the bad, now in the days of his youth even before he is able to know the reason why; and when reason comes he will recognize and salute the friend with whom his education has made him long familiar... (401C-402A)
The "friend" referred to is reason, both in intellectual and practical matters, by which Plato means a harmony of the soul in its engagement with any sort of human problem, resolving discord and chaos into something beautiful in thought or action. Reason is therefore a kind of "musicality" in the person.
11
The ancients, or at least some of them, took the idea of musical therapy seriously, as the following passages will show. Plato's talk about beauty flowing into the soul is not entirely metaphor. Rhythms and melodies were taken to exercise a strong influence on both soul and body, as is shown by the following citations of ancient sources in W. Tatarkiewicz, History of Aesthetics, I, p. 87-88.
The Pythagoreans, whom Plato follows in many respects, call music the harmonization of opposites, the unification of disparate things and the conciliation of warring elements. For they claim that not only rhythms and melody but in fact the whole system [of the world] depends on music, whose object is unity and harmony. God harmonizes warring elements and this in fact is his greatest aim in music and the art of medicine, namely that he reconciles things which are hostile. Music, as they say, is the basis of agreement among things in nature and of the best government in the universe. As a rule it assumes the guise of harmony in the universe, of lawful government in a state, and of a sensible way of life in the home. It brings together and unites. They say that the effects and application of [musical] knowledge reveal themselves in four human spheres: in the soul, in the body, in the home and in the state. For it is these things that require to be harmonized and unified. (Theon of Smyrna, Mathematics I)
It is said they [the Pythagoreans] employed incantations against certain illnesses; they assumed that music also has a great influence on health if is it used in a proper way. They also used the words of Homer and Hesiod to repair the soul. (Iamblichus, Life of Pythagoras, 169)
(e) Beauty and Pleasure
Everyone tends to think that there is an intimate connection between beauty and pleasure. The Greeks were certainly no exception. Yet to equate the beautiful with the pleasant seems to miss the ideal character of the beautiful, since not all pleasure seems good enough to testify to a thing's beauty. This problem figures in Plato's late (and huge) dialogue, Laws. In book II 659A he says that only the pleasure of a person "pre-eminent in virtue and education" can serve as a working criterion of the beauty of a choral work or performance.
Elsewhere , in the Philebus 51B-D, he distinguishes interestingly between sorts of pleasure in a context which implies that some of them are better indicators of beauty than others. Some pleasures are mixed with pain or displeasure, as when we satisfy our thirst. The relief produced is very pleasant, but it also contains a diminshing element of displeasure, namely the discomfort which we have not yet fully relieved. This shows itself in the eager haste with which we drink after long thirst. In contrast to these mixed pleasures are the pure or true ones, described this way.
12
True pleasures are those which are given by beauty of colour and form, and most of those which arise from smells; those of sound, again, and in general those of which the way is painless and unconscious, and of which the fruition is palpable to sense and pleasant and unalloyed with pain .... When sounds are smooth and clear, and have a single pure tone, then I mean to say that they are not relatively but absolutely beautiful, and.have natural pleasures of the same character ...I do not mean by beauty of form such beauty as that of animals or pictures, which the many would suppose to be my meaning; but, says the argument, understand me to mean straight lines and circles, and the plane or solid figures which are formed out of them by turning-lathes and rulers and measurers of angles; for these I affirm to be not only relatively beautiful (1), like other things, but they are eternally and absolutely beautiful, and they have peculiar pleasures, quite unlike the pleasures of scratching. And there are colours which are of the same character, and have similar pleasures; now do you understand my meaning? ...The pleasures of smell are of a less ethereal sort, but in having no necessary admixture of pain, in the manner in which the enjoyment is felt, and the subject which feels it, in all this I deem them analogous to the others. Here then are two kinds of our unmixed pleasures....
[(1). By relatively b'ful in this context Socrates should mean apparently b'ful, due to a distorting condition in the subject; and by absolutely b'ful he should only mean genuinely or objectively b'ful, not perfectly or supremely so, since that is the logical negation of the first. Refer back to the distinctions in the Introduction.]
Here once more we have a case of Plato's slipping from his strict doctrine that only abstract things can be absolutely beautiful. The cylinders and newel -posts turned out by lathes are full of impurities compared with the flawless Forms. So he should have said here that the lathes produce shapes that are nearly perfect concrete instances of geometrical Forms. They may be as beautiful as concrete particulars of that sort can be, but they fall short of the ethereal beauty of the Forms. The confusion may arise from the fact that physical shapes carry the mind to those geometrical Forms far more forcefully than less regular shapes could, for instance the more mixed, less pure, configuration of lines making up a human face. The delight we feel in looking at precisely machined products derives therefore from an intellectual delight in the Forms themselves.
But what of pure colors, tones, and aromas? Can these be understood as giving purely intellectual pleasure? Don't they (especially smells, as Socrates concedes) give sensuous pleasure? Here Plato is probably influenced by the idea that the mathematical properties of vibrations cause the effects of purity of tone and harmony. Probably Plato thought the same of colors, though there was no proof of that in his time. As to smells (and flavors), the data of the "chemical" senses, the mathematical case can't be made out even now. Yet many Greek thinkers, probably including Plato, thought that pure sensory pleasures result from some sort of good proportionality between the sensory property and the human soul, and this proportionality could of course be admired intellectually. But one wonders how the pleasures of colors or smells could possibly be reduced to that, since our senses can't actually present the proportion to us for admiration.
And is Socrates right to believe purely intellectual pleasures are wholly free from the distorting relief or contrast effect? Clarity of form is arguably pleasing partly because it relieves us of confusion and uncertainty.
13
Applications of Platonic principles: Plato's normative aesthetics
In order to give more concreteness to the general terms used by Plato, study of particular cases is in order. Here we face a difficulty, however. Too little is known about Greek music to give concrete examples, and unfortunately the art to which Plato looks most affirmatively for the beautiful is music. Much of the treatment of literature and the visual arts is negative, so that it is hard to find clear indications of what Plato admires aesthetically in them -- that is, what specific artistic effects he admires most and in what sort of examples. Still, some reasonable suggestions may be based on his general remarks positive and negative. That is, we can suggest what seems to follow regarding some traits of Greek art. Architecture seems a good place to begin, followed by the admittedly homely example of pots. In both these cases a geometricizing intention can be given fairly full rein, and was. From them we will proceed to pure geometry, specifically to the famous "golden section" which figures prominently in Greek art theory. Then we will turn from art and mathematics to nature, with an excerpt from Plato's dialogue Timaeus in which he puts forward the idea that the beauty of the natural order derives from the elegance of its geometry -- specifically of its elementary particles and its large-scale structure. Finally a non-mathematical example of intellectual beauty will be given from a modern theory of justice which appeals to rationality in a way that seems eminently compatible with Plato's ideals, however discordant the theory is with Plato's own preferences in social and political matters.
(a) Greek temple architecture
The geometrical character of Greek temples is immediately evident. The floor
plan speaks clearly of this, as in the case of the Parthenon in Athens:
For centuries Greek temple facades were considered the prime instances of geometrical purity in architecture . Alterations after the classic period were few and slight. Time and again the classic "orders" -- that is, the different standardized designs of facades -- were revived and used in a wide variety of applications, mny of them quite remote from their original context. Next chance you get, compare the Supreme Court building, which is essentially a Greek temple, with the Capitol, which uses a temple facade as a small element in the mass of its huge front. That will make the point more gracefully than the buildings on campus, which, aside from several small exceptions, are a case study in the degradation of a noble idea.
14
Regardless of what Plato would have said about the Parthenon had he ever written an aesthetic critique of it, the sense of clarity, order and harmony which it and many other such structures awaken in viewers is deeply in accord with his stated principles. So in that way such structures must be good, even eminent, cases of architectural beauty by Platonic standards. The widespread use of the same forms for centuries is also Platonic in spirit. Plato condemns the thirst for novelty for its own sake. The beautiful things are the best things, and the best things should be retained, cherished and replicated as far as possible.
So far, the application of Plato's idea is straightforward. But there is another aspect of the best Greek temple design which is at odds with the geometrical. The most highly refined temples were not left geometrically pure but in various ways were modified or "tempered". The entire floor (stylobate) was arched, as were the steps. The columns were slightly tilted, the corner columns made slightly thicker than the others. All the columns bulged slightly in the middle, and the pediment above them was tilted a bit forward. The Parthenon is the preeminent instance of all this. No expense was spared in perfecting the refinements of this monument to the splendor of Athenian imperial power. Here is a rendering of the result,- in which the temperings are exaggerated for legibility. The illustration is taken from W.Tatarkiewitz, History of Aesthetics.
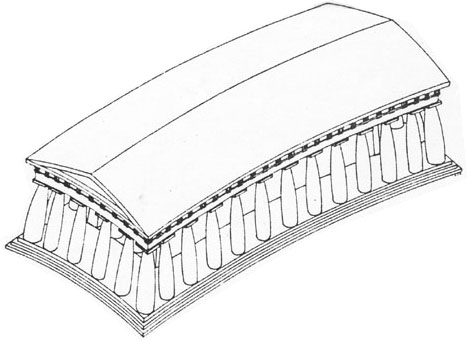
From a geometrizing point of view, these refinements were distortions of a
profoundly anti-Platonic character. Not only do they destroy the simplicity
of the architecture, but their purpose is mainly to achieve the visual effect
-- the illusion -- of geometrical purity. This is clear from the words of Philon
of Byzantium, a late 3rd century B.C. writer. Further the needed deviations
were arrived at by empirical methods, by trial and error, not by pure thought:
15
For it was not possible to create the [proper] forms of buildings from the start, without first engaging in experiment, as is clear indeed from ancient buildings, which are extremely unskilful not only in construction, but also in the design of forms for the individual parts. The change to what was required was not the result of a single or random experiment; some of'the individual parts of'a building, although they were in fact of equal thickness and straight, seemed to be neither of equal thickness nor straight, because our sight is misled in such matters by differences in distance. So by trial and error, by adding to and subtracting from the sides, by taperings, and by all sorts of'experiment, they made them [i.e. the parts] in accordance with vision and apparently well-shaped; for this was the goal in that art.
The implications for Plato are intriguing. On the one hand Plato recognizes that in social policy one must make concessions to the limitations of human senses, which are inherently incapable of seeing things as they are. Perhaps, then, Plato might say it was better to make the temples look beautiful rather than be beautiful. The false appearance of beauty, even if an illusion, conveys to the mind the image of beauty better than a true appearance of it. Thus the philosopher might accept the falsehood as a "noble lie", as he called the mythic fabrications in the Republic that aimed at social benefit. He might even find in such fitness for its purpose a sort of beauty.
On the other hand, such impurity is bound to be galling to the idealist in Plato. For after all, the refinements taken collectively are geometrically unbeautiful, perhaps even ugly. In this respect the Parthenon is bound to be obnoxious to Plato's enlightened viewer, who prefers to live in the presence of a truly beautiful building even if its beauty is not available to his eyes, that is, even if it looks ugly because it makes no concessions to the senses. (Or maybe a wiser enlightened one would dwell on the idea of a perfectly geometrical building instead of gazing at the actual structure.)
The tension implicit in the predicament is complicated by the presence of another factor. Some of the convexities in actual temples go beyond what is needed to counteract perceptual illusions. Modern architectural historians think that the motivation for this excess is to relieve the rigidity of the geometry a bit by subtly making the forms seem expansive. Convex volumes seem slightly to press outward, thereby imparting a feeling of vitality to the forms they bind. Would Plato have considered this practice another deviation from rationality, an unfortunate concession to our animal nature, which craves forms expressing its sort of vitality? Very likely, since unquestionably it involves illusion. Worse, suggestions of animal vitality interfere with the expression of the higher, purely intellectual vitality of the rational mind in vigorous pursuit of pure form. On the other hand a temple is a civic structure meant to uplift a public unlikely to be moved by rigid geometry. We can only conjecture how Plato might have dealt with the resulting dilemma. Accordingly our reconstruction of his normative aesthetics must remain indefinite in this respect.
(b) Greek pots
Students of Greek pots have sometimes charted the geometrical properties of these homely artifacts. These also remained true to type for centuries in Greek and Roman culture. According to Tatarkiewicz, the following are honest examples of geometrically regular proportions. Those on the first row obey a rule of the square, those on the second a rule of the golden section.
16
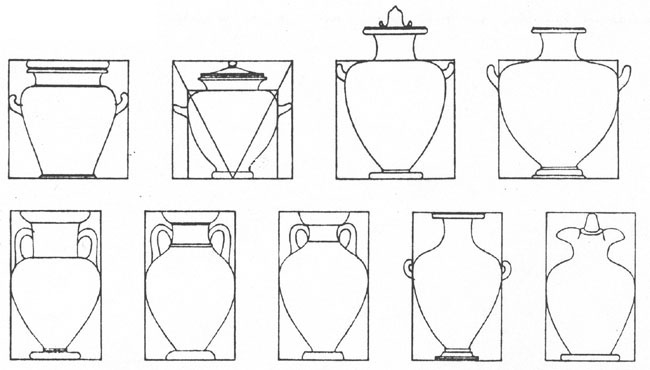
Other authorities are less supportive of the main idea, stressing the irregularities to be found in the manufacture of pots and vases, even the finest. But waiving that for the moment, let us consider what would be beautiful about pots produced by the law of the square. First, what is beautiful about a square? Its regularity, is the standard answer. At first glance this amounts to the equality of sides and angles. But there is more: from that initial set of equalities flow others. Diagonals produce equal isosceles triangles, perpendiculars from whose vertices create equal squares, repeating the pattern. Equalities proliferate endlessly, precisely, proportionately. Every region of the square divides into an infinite regression of squares. What at first looked like blank, unordered space is revealed to be dense with precisely ordered, uniformly distributed equalities
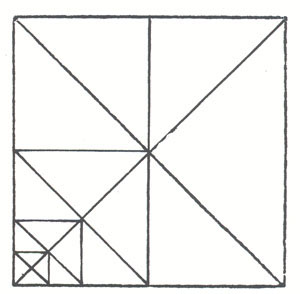
17
But even granting all that, do the square's equalities produce beauty in pots?
If so, how do they do it? Clearly, any pot conforming to the rule of the square
must have bilateral symmetries endlessly divided. For each region, however small,
on the right, there must be a region on the left precisely mirroring it. This
will rule out pots that are uneven, tilted, etc., and include a great many of
the pots anyone would think beautiful. But the idea behind the rule assumes
more, namely that pots conforming to the square are superior to those of a near-square.
Thus the pots in our top row should be superior to the slightly widened or narrowed
variations.
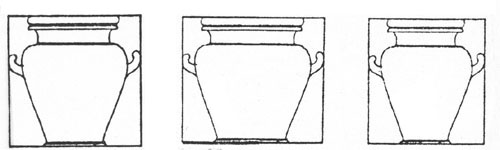
It is not hard to see the difference in the three. But is it so easy to detect a difference in beauty?
If (a big if) the "square" pots are superior to the near-square ones,
the next question is, what is it about the square's equalities that makes the
pots beautiful. An obvious suggestion is that there are more equalities in pots
which obey the law of the square than in (symmetry-preserving) deviations from
it. Such an hypothesis might be tested by comparing variations on the second
pot from the left in our original row with the original:
Or by comparing the examples in the original row with each other. Are they
all equally beautiful?
18
But then again, maybe such tests will fail or leave us in doubt about the significance of the beauty-making power of such geometry.
(c) The golden section
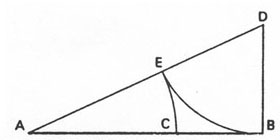
Industrial applications aside, there is no doubt of Greek intellectuals' fascination with mathematics -- with pure mathematics, that is. One especially prized example of elegance in mathematics is the golden section, which was the division of a line into segments such the shorter stands to the longer as the longer does to the whole (that is, to a+b, the sum of the segments). In the illustration below a is the longer segment, which stands to the whole as the shorter, b, stands to it. C marks the golden "cut".
A___________a____________C________b________B
In this section I draw from H.E. Huntley's The Divine Proportion (1970),
which lays out a truly impressive profusion of applications of the golden section.
The numerical value of the ratio (a: b, (a+b) : a) is 1.61803....Toy
with the simple diagram above and one finds that the ratio immediately produces
remarkable replications of itself. If we fold segment b (count that as
= 1) back into a we obtain a golden cut of a at C'. Folding
the shorter of the two resulting divisions of a back into a produces
a golden cut of that section. Repeating the process yields smaller golden cuts
endlessly. Or going the other way, extending a+b by a segment equal to
a makes A the golden cut in the line extended line AD.
That process can also be endlessly repeated, golden cut after golden cut. Neat.


19
Golden sections can be constructed by the simplest of means, a straight-edge and a compass, thus: if AB below is a given straight line and BD is a perpendicular = AB/2, then, AD having been joined, an arc with radius DB can be drawn cutting AD at E and another arc with radius AE cutting AB at C. C will then mark the golden cut of AB.
That's just the beginning. Next one moves on to golden rectangles, which are ones whose adjacent edges stand in the ratio of the golden section, as in the figure below; left; and thence to the golden cuboid, a rectangular parallelepiped four of whose six faces are golden rectangles (all except the front and back of the figure below, right.
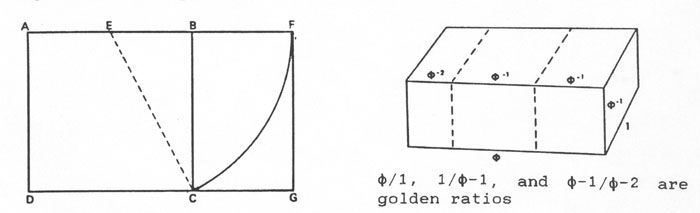
To construct the golden rectangle, above left, one begins with a square
ABCD; then, bisecting AB at E, one draws an arc with radius EC, cutting the
extension of AB at F; FG is drawn perpendicular to AF meeting extended DC at
G. Voila. The golden cuboid is readily constructed from golden rectangles,
as may be seen from the indications on the diagram.
20
Rectangular polygons (plane figures with all sides and all angles equal) are
full of golden sections. Diagonals of a pentagon cut each other in golden sections,
as in (c). The radius of a circle circumscribing a regular decagon (ten-sided
polygon) stands in the golden ratio to each of its sides, as in (d).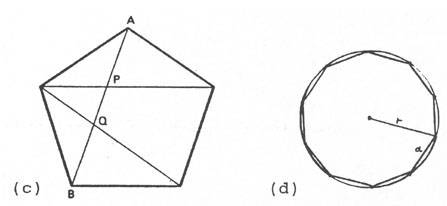
The five regular solids are replete with golden sections. The icosahedron's
vertices form the corners of three perpendicular golden rectangles, as in (e);
while the dodecahedron's faces are connected in a similar way, their centroids
being the corners of three golden rectangles, as in (f).
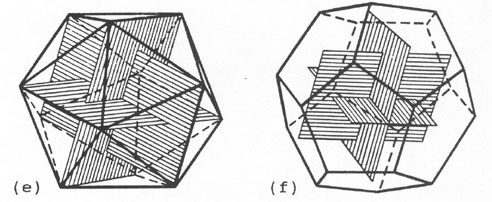
21
A particularly attractive aspect of the golden ratio comes to light in relation
to additive series of squares. Starting with two arbitrarily chosen squares,
1 and 2 in (g), an endless construction may be projected in which the side of
each square after these is the sum of the sides of the previous two, as in (h)
. This produces rectangles which endlessly approach the golden rectangle. Further,
if one connects the centers of the successive squares with a smooth curve, one
finds it is an elegant logarithmic spiral. Alternatively, one can start with
a golden rectangle ABCD, as in (i), and construct (by straight-edge and compass)
a descending series of golden rectangles within the first, EBCF, HGCF, HIJF,
HIKL, etc. The limit of this series is 0, the pole of a logarithmic spiral which
passes through the corners (J, G, E, D) of the successive golden rectangles.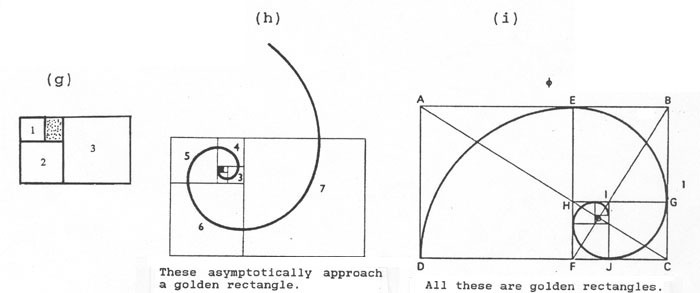
Similar elegance is discovered in the case of the golden triangle, an isosceles
triangle whose sides stand to the base in the golden ratio, in (j). The bisectors
of the base angles cut each other in golden sections at E, and cut the sides
opposite them into golden sections,. as at D. Further, the triangle formed by
CDE is a golden triangle. One can then perform the same operations on that triangle,
producing EFG, and replicate the process endlessly. Equally we can go in the
other direction, obtaining an endless series of golden triangles or larger size.
Amazingly, their base apexes will define a logarithmic curve.
Furthermore, the triangles in (j) obey a "Fibonacci" rule. That is, the sides of the successive triangles are GF = 1ø, FE = 1ø + 1, ED = 2ø + 1, DC = 3ø + 2, CB = 5ø + 3, BA = 8ø + 5,...

22
Multiple golden sections are also found in the mystic pentagram, which was used as a badge of the Pythagoreans in ancient times. Since the pentagram is produced from the pentagon, the prolongation of whose sides produces golden triangles, as in the case of A'B'D' and D'ST in diagram (k), there is a mind-boggling profusion of golden sections as well as a logarithmic spiral. Shazaam!

Huntley's revelations go on and on. There is seemingly no end to the fertility of this remarkable ratio. Unquestionably it is beautiful from a mathematical point of view -- as countless other ratios are not. At random: 1/14 is humdrum, 1/(4) + 14) is relatively insignificant. Even 1/1, the ratio of the square, is distinctly less potent in producing complex elegances. Complex figures reveal a deeper rationality than we could have anticipated when their relation to this ratio is grasped. All very Platonic, very Apollonian.
(d) The structure of the cosmos
Plato's cosmology is another instance of the application of his ideas of beauty to concrete particulars. Two small extracts will make the point. First, according to the myth in the Timaeus the world creator "looked to [an] eternal pattern (i.e. to a perfect Form]" with the result that "the world is the fairest of creations". It "has been framed in the likeness of that which is apprehended by reason and mind..." In the likeness of, not identical with, for the latter is impossible. There are two basic types of created things, material things and souls. The material things are perceptible, the souls not. But the soul of the world as a whole must have the same form as the large structure of the cosmos or else the cosmos could not be governed by the soul, Plato says. So the structure of the heavens and the structure of the world soul are the same. One diagram does for both. Hence astronomy gives not just the structure of the heavens but also some of the theology of the universe. The heavenly bodies are besouled, as the names of the planets imply.
23
Now the world as a whole, body and soul, is a sphere "round as from a lathe, having its extremities in every direction equidistant from the center, the most perfect and the most uniform of all figures; for [the creator] considered that the like is infinitely fairer than the unlike..." The world regenerates its own wastes, "For the creator conceived that a being which was self-sufficient would be far more excellent than one which lacked anything." The only overall motion allowed to this universe is motion in a circle, turning on its axis, soul and body together, since that "is most appropriate to mind and intelligence". (Timaeus 33-4) The heavenly bodies within the spherical universe (i.e. the stars and planets) are also as perfect as possible, hence spherical (that is, the stars and their souls, the gods). These heavenly beings are spaced in beautiful mathematical ratios: 2:1, 3:2 and 4:3, which are harmonic ratios (octave, fifth, fourth). Here is the result. [Note: Planetary and solar orbits are helices because the bodies are higher in the sky in summer, lower in winter, transcribing a helix with fixed (cylindrical) diameter ].
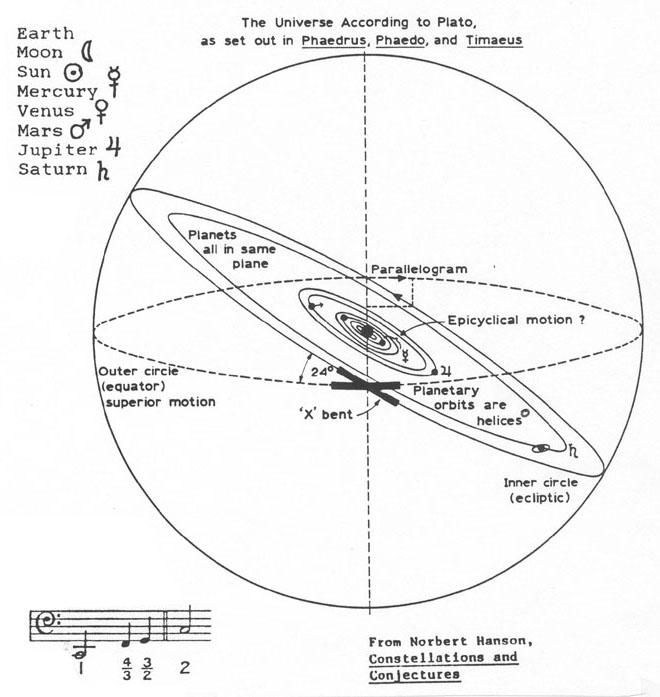
24
The creator aligns the body and soul of the universe with one another.
Now when the Creator had framed the soul according to his will, he formed within her the corporeal universe, and brought the two together, and united them centre to centre. The soul, interfused everywhere from the centre to the circumference of heaven, of which also she is the external envelopment, herself turning in herself, began a divine beginning of never-ceasing and rational life enduring throughout all time. The body of heaven is visible, but the soul is invisible, and partakes of reason and harmony, and being made by the best of intellectual and everlasting natures, is the best of things created.
Like the creator in Genesis Plato's looks at the result and approves:
When the father and creator saw the creature which he had made moving and living, the created image of the eternal gods, he rejoiced, and in his joy determined to make the copy still more like the original; and as this was eternal, he sought to make the universe eternal, so far as might be. Now the nature of the ideal being was everlasting, but to bestow this attribute in its fulness upon a creature was impossible. Wherefore he resolved to have a moving image of eternity, and when he set in order the heaven, he made this image eternal but moving according to number, while eternity itself rests in unity; and this image we call time.
Thus the cosmos. The second example of mathematical harmony in the world is
the inner structure of the four physical elements, earth, air, fire, and water.
They are composed of particles having different geometrically perfect shapes
built up out of two right triangles: (a) a half-equilateral isosceles triangle,
and (b) a half-square. From such "sub-atomic" elements are obtained
triangles and squares of different sizes, which in turn combine to form the
faces of particles. Below is the reconstruction of this found in F.M. Cornford,
Plato's Cosmology, pp. 210ff.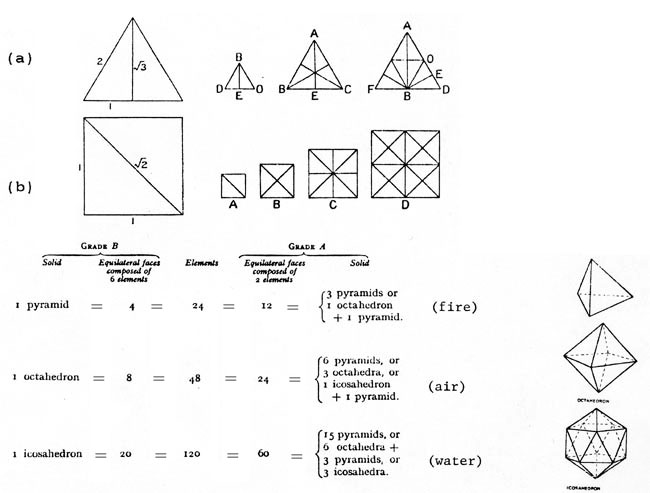
25
Because these particles are built from the same basic form, transformations of one into another occur, but none of them can be transformed into an earth particle, which is built up from the half square.
Plato's vision of the structure of matter is therefore far more rationalistic than that of the Greek atomists such as Democritus or Leucippus, whose atomic elements were of indefinitely many forms. Where they saw a chaos of diversity Plato saw an elegant order, as befits the creation of a divine craftsman, the Demiurge (the Greek word means craftsman). Plato's (entirely speculative) physics is an early example of theory building driven by a principle of method now universally adopted by science, namely that one seek the simplest hypothesis which accords with the known facts. Mathematical simplicity is a prime value in science, though of course present theorists must draw upon much more complex mathematics than Plato's to accommodate the vastly expanded set of empirical data. In this way mathematical beauty is widely recognized to be an important principle of selection among theories which explain the same facts.
Clearly Plato would count universes beautiful in proportion to the pervasiveness of mathematical beauty within them. By a parity of reasoning he should rate substances and creatures within the universe by the same criterion, so far as physical beauty is concerned.
(e) Colors and sounds
The mathematical basis of sonic harmonies has already been mentioned. What of single tones? Pitch alone seems to provide no basis for judgment. Presumably Plato would count all pitches equal in beauty, other things being equal. The (degree of) beauty of a tone would depend on variable properties such as purity. Non-pure tones might be ranked on the basis of the harmony or dissonance of the overtones that make up the whole sound, giving what is called timbre or tone color. Lots of interesting problems of detail arise here. The tone color of different instruments, a violin as opposed to a flute, for example, involves not only overtones but an admixture of noise, which is unorganized sound, as in the scraping of the bow on the string or the breath of the flautist. How are these contaminants to be assessed? All we can safely infer from Plato's general Apollonian perspective is that contaminants are worse in proportion as they lack some compensating tendency toward the rational in a broad sense of that term.
The Greeks knew of no mathematical basis for color, and the vast advances moderns have made in understanding it provide no great encouragement to the idea that color harmony can be explained in terms of simple mathematical ratios. A Platonist must deal with color qualitatively, seeking analogues of rationality and rejecting analogues of unbridled passion. This will favor colors which are pure, distinct, and harmonious and disfavor those that are clashing, muddy, dull, etc. Brightness, transparency and pattern-clarity have an obvious connection with the rational virtues which are basic to Apollonianism. Designs whose colors conflict with each other in eyebefuddling ways, blanking each other out, or melt into each other indistinctly are correspondingly defective, from Plato's point of view. The venerable neo-classical traditions in painting and decoration long promoted such color properties, vying against Dionysiac color -- as in Baroque exuberance or romantic sensuality or moodiness.
26
(f) Justice and rationality
To the foregoing the insightful reader may object that mathematics has no obvious relevance to lots of things that Plato, and we, want to call beautiful. Ethical ideals, for example, which are certainly regarded as beautiful by Plato. This is evident from Diotima's speech in the Symposium. Now in fact Plato seems to believe that justice, temperance, etc. in the soul -- in the sense of a settled disposition to seek and the mental skill in finding and the practical wisdom of figuring out the right way to put into practice a just or temperate solution to matters of dispute or choice -- is derivative from a mathematically harmonious condition within the soul itself. But that is a dubious hypothesis at best. So it is relevant to offer an illustration of how one of these virtues could be thought intellectually elegant without any reliance on mathematics. In our own time philosophers and students have spent millions of brainhours discussing a theory of justice by John Rawls (A Theory of Justice), which seems admirably suited to this purpose. Its central principle is amazingly simple, and in consequence the virtue of justice on Rawls' theory has a non-mathematical elegance comparable to the mathematical beauty possessed the four natural elements on Plato's theory of matter.
The kernel from which Rawls' theory springs is a thought experiment which imagines ideally self-interested persons deciding among themselves what sort of social framework to adopt, but doing so prior to knowing what sort of natural and man-made advantages they will turn out to have within the society governed by that framework. They do not know whether they will be smart or stupid, born rich or poor, surrounded by helpful or nasty persons, in a country which is powerful or impotent. They only know what sort of human desires and tendencies there are in general -- they know human psychology -- and what natural laws there are in the physical world. Thus they must decide behind a "veil of ignorance" (of their personal situation). Now if they are perfectly rational and self-interested, they will want to maximize their chances of happiness and minimize their chances of misery whatever their situation turns out to be. Therefore they will choose the social framework which is ideally fair to everyone regardless of his or her natural advantages or disadvantages. That framework is, says, Rawls, the ideally just system.
For our purposes it is not necessary for this to be a true theory, or even to be Rawls' full theory (I have simplified it a lot). It is only needful to appreciate that if such a core idea were capable of generating decisions about social orders that better satisfied our best, most reflective intuitions of justice than any competing theory, then justice would emerge as a beautifully elegant concept. We all know how fearfully complicated the hard questions of justice can be, and if such a simple but far-reaching idea could be shown to give compelling answers to those questions, then justice would be amazingly, really amazingly, coherent. For such a simple core to ramify into such a dizzing multitude of consequences would supply us with rationality beyond our wildest expectations. It also offers hope that more of the vast sea of beauty can be brought within the scope of Plato's theory than one would think, by further explorations into non-mathematical forms of rationality.
27
Plato's theory once more: back to the ontological core
After familiarizing ourselves with the theory and its applications we now return to the core concepts to deepen our understanding of them. We must more closely define the characteristics of beauty as a Form, their objectivity and the grounds for ascribing to them the extraordinary degree of beauty which Plato claims for them.
(a) Abstract Forms, concrete particulars and things between
A nicely documented thumbnail summary of Plato's claims about Forms is given by a recent writer on Plato's theory, Richard Patterson, Image and Reality in Plato's Metaphysics:
The characteristics distinguishing Forms from other sorts of things are familiar, if not always well understood. Forms are invisible, intangible. wholly insensible, and accessible in their purity to pure reason alone (Phaedo 65d9-66a7, Phaedrus 247c6-9. Timaeus 27d-28a). They are immutable, not subject even in principle to any sort of becoming or change whatever (Phaedo 78d-79a, Symposium 211a. Timaeus 27d-28a); they do not even grow older with the passage of time (Timaeus 38a). Forms are not in any place at all, and so are not divisible into spatial parts (Timaeus 52a-b, cf. Phaedo 78c, 80b-c). Each is incorporeal and pure (eilikrines, katharon) of admixture with any sensible or any opposite it may have (Phaedo 66a, 74 b-c Symposium 21la. Republic 477-480, Philebus 59c). And each Form is in some sense "single-natured" (monoeides) rather than "multiform" (polyeides; see Phaedo 7845, 80b, Symposium 21lbl).
All these descriptions circle around the idea of abstract-concrete distinction without pinning it down precisely. The ontological distinction which lies at the heart of it can be best explained by focusing on the idea of concreteness. What is the essential requirement that anything must meet if it is to be a concrete particular? The answer (never fully articulated by Plato) is that it must have a fully specific set of determinations: nothing must be left in any way or degree general. For example, the oak tree to the right of my front door must have roots, trunk, branches and foliage of a fully determinate shape, size, color, molecular structure, etc. at any given moment of its life, an exact spatial relation to each and everything else at each given moment, a fully particularized history of coming into existence, changing over time, and going out of existence, etc. There must be nothing vague, unspecific, indeterminate about it.
Forms on the other hand are abstract in precisely the sense of always being comparatively indeterminate or unspecific -- in that there is always some other more specific Form of that sort, or else in that there is, or could be, a concrete exemplification which is more determinate. Triangularity, for example, has isosceles, scalene and obtuse as further specifications. These compound Forms have their own further possible specifications -- e.g. isosceles triangularity with base angles of 30 degrees. And though Plato's thinking about the Forms never seems to have been carried this far, the sequence of increasingly specific Forms would seem to continue all the way to the limit, which is entire determinateness save for spatial location, temporal history and all that is entailed by them. If there is a Form of oak tree in general, there must also, it seems, be an oak-tree Form defined in terms of the totality of specifications which happen to be fulfilled by the oak tree to the right of my front door at the present moment except those that concern spatial location and temporal history. The world of Forms, it seems, must be extraordinarily multitudinous.
28
Plato's best pupil, Aristotle, further nailed down the difference between the abstract and the concrete by a logical differentia. Abstracts, he said, can be either subjects or predicates of propositions, but concrete particulars can only be subjects, never predicates. For example, beauty can be either a subject (as in "Beauty is generally pleasurable" or "Beauty is never perfectly exemplified in concrete particulars") or a predicate ("Justice is more beautiful than injustice, other things being equal"). But a concrete particular, Socrates for example, must always be a subject (as in "Socrates is the father of Sophronicus"). It (or he) can never be a predicate. Try thinking of a person as a predicate and you will see there's an absurdity in it. You can imagine being like Socrates or even being Socrates, but you can't imagine having Socrates as a property.
From the basic distinction between abstract and concrete things follows a third differentia. Forms that are definable (that is, are not logically "primitive") are defined by their "essential" constituents (the "specifications" to which I have alluded), as for instance triangularity is by three-sidedness and plane-figurehood. From such a definition plus the axioms of geometry all the relations of the Form to other Forms are deducible (all the theorems about triangles, for example). But no concrete particular can be comparably defined. There is no statement of the essential properties of the oak tree to the right of my front door that permits deduction of all truths about its relations to other concrete particulars (e.g., that this house will stand next to it, that this grey squirrel will nest in it).
To understand the abstract-concrete distinction really well requires also that we realize that Forms and concrete particulars do not make up all there is. Between Forms and concrete particulars lies a gap which is occupied by a third ontological type. For consider: Forms are completely indeterminate as to place and time. Concrete particulars are completely determined spatially and temporally. 'Between these polar opposites is room for things partially but not wholly determined by space and time.
And we find such things. Works of the performing arts, musical compositions, for example, and literary works fill the bill. A novel is a perfectly specific sequence of words, punctuation signs, etc.-a determinate text (at least in the ideal case). But this text is still abstract, since it is concretized in printed copies. Each copy of the novel is a concrete particular with a completely determinate history in the world. Each is a copy of the novel, an instance of it, which makes the it, the novel, abstract. But the novel is not purely abstract, for the text exists as such only within a historically concrete culture. It is furthermore the product of one person (or one team of persons) uniquely --for example, it is Saul Bellows' novel, uniquely his creation (perhaps with some input from an editor). Had anyone else at some different time, by an incalculable miracle, independently produced the same string of words, there would be two texts; two novels, not one -- like identical twins, who are different persons. So a novel is a hybrid sort of thing, a "universal-cum-particular" as it is sometimes called (cum being Latin for with). As just a moment's thought will show, there are many, many such things, in art and outside of it (my signature, your smile, his idea, etc.).
So: Forms are purely abstract -- they have no space-time determinations regardless of how specific they may be in other respects. Concrete particulars are purely concrete -- they have a fully specific set of determinations including sharp locations in space and time. And hybrid things are partly abstract and partly concrete.
29
From the pure abstractness of Forms follows an interesting consequence. In one clear sense of the terms, Forms are neither mental nor physical. That is, the property itself, the Form, is neither a mental thing - a thought or feeling -- nor a physical existent, a brain event or blueprint. To be a mental or a physical thing in this sense is to be a concrete particular of the mental or physical sort. Of course in another sense some Forms are "mental" in that they may be such that only mental things can exemplify them, as is the case with self-doubt -- and some are physical in a corresponding sense, such as weight or mass. Here we are dealing with properties of mental or of physical things. And we abbreviate this as mental or physical properties. But the naturalness of this way of speaking does not entitle us to the conclusion that the properties themselves are mental or physical things -- things in the mind or in the physical world.
Note. In some passages, notably in the Allegory of the Cave in the Republic Plato strongly suggests that only Forms are real, or fully real, and that concrete particulars are illusory or imperfectly real. In the present context I set this (highly implausible) idea aside since it is not at all clear how it could affect questions about beauty or even questions about the key ontological differences between concreteness and abstractness. Remember, the aim here is to discover the most plausible form of Platonism about beauty, not to dwell on every detail that survives from the historical Plato.
(b) Characteristics of Beauty
Now consider Beauty in particular. At the very outset we laid down as truisms a number of properties of beauty which we can presume Plato accepted or would accept if they were presented to him. To wit:
i. it is a supervenient property
ii. it is a property of degree (a comparative property)
To these we can add the following, variably contestable principles which our study of Plato's texts has revealed he believed true. Beauty is a Form (with all that entails) such that
iii. its exemplifications typically are recognizable by mere inspection and reflection, whether rational or sensory, and typically are lovable.
iv. its degree varies according to such Apollonian criteria as purity, completeness, and rationality (using rationality to cover simplicity, clarity, proportionality, etc.). Beauty is Apollonian.
v. it exists in higher degree in abstractions than in concrete particulars, and in the highest degree in Beauty itself. Beauty Itself is maximally beautiful.
vi. it is a unitary property.
30
Taking these as our starting point, let us now dig deeper in two ways, adding other properties and delving further into the ones already cited. One crucial addition is this: beauty for Plato seems to be an inherent or response-independent rather than response-dependent property. The basic idea of this category is that of a property whose description involves no reference to the relations of response holding between it and other things. For example, "triangular" is a property of a geometrical shape, whereas "envious" is a relation of response. This shows in the fact that "X is triangular" is a complete expression whereas "X is envious" is not: X must be envious of someone or some thing Y. In the case of beauty, a response-dependent theory might hold that beauty was a relation between a person and an object, such as the object's being aesthetically attractive to the person under specified conditions.
Since the Symposium describes beauty as being what it is (a) regardless of our opinions and feelings, (b) without limitation to a point of view or context ("not fair from one point of view and foul from another, or at one time or in one relation"), indeed as being (c) "absolute, separate, simple," it is plausible to infer that Plato believes it is an inherent (i.e., response-independent) property. Hence we may add that to the list of essential properties of beauty
vii. it is an inherent (response-independent) property, not a property of (aesthetic) response.
Here a number of cautions are in order. First, properties are not made response-dependent because people happen to respond to them. The question is whether that response is a necessary condition of the property. Also it is essential to realize that the non-response-dependency of beauty isn't shared by many other Forms. Response-dependent Forms are common enough: pleasantness, frighteningness, sexiness, for instance. Further, some such Forms can be beautiful. Clarity and intelligibility are response-dependent in that they imply an intellectual response of understanding given the presence of a reasonably capable thinker. It's just that their beauty can't depend on whether or not people appreciate their beauty.
In beautifully coordinated dances or beautifully composed paintings or beautifully amiable and lively conversations, it is in large part the responsiveness of the participants to each other that is so beautiful. Beauty supervenes on such responsiveness. Still on Plato's view that beauty does not depend on others seeing it for what it is.
We will encounter response-dependent notions of beauty very soon. These identify beauty with the power to elicit a favorable aesthetic response under optimal conditions.
Proceeding to other essential beauty-characteristics, a consequence of v. above deserves close consideration. If the Form Beauty is itself beautiful then Beauty must be a rather special sort of property, namely one which can have itself as its own property. It must be a self-exemplifying property. This sounds weird when put this way: a property which has the property that it is. The oddity is disguised by the misleading formula, beauty is (of course!) beautiful. But what is implied by that formula is not the empty tautology, beauty is beauty (beauty = beauty), but beauty is beautiful-- the is is the is of predication, not that of identity. And this -- beauty is beautiful -- is deeply puzzling. For properties typically do not, cannot, have themselves as properties. Humanity cannot be a human, cancer cannot have cancer (would that it could), the property of being money cannot buy anything, and so forth. Why then should beauty be beautiful?
31
To find one's footing here, one must first recognize that some properties are self-exemplifying. Abstractness is abstract (though concreteness is not concrete). Thus one cannot rule out the possibility of beauty being beautiful without some further reason. But by the same token Plato will need some reason for contending that beauty is beautiful (and more yet for its being the most beautiful of all).
Plato seems to regard the statement that Beauty is beautiful as self-evidently true. He seems almost to mistake it for the identity statement, beauty = beauty. But, as we have seen, to take it so would make it trivial, which would be deeply antithethical to his intent. Hence he must ground the self-exemplification thesis in some other way or else give it up.
Thinking about this seriously soon shows us how out of our element we are in aesthetic criticism of abstractions. What sorts of beauty can properties have? Especially highly general properties? They can't have nice colors or shapes. They can't sing sweetly! How then are we to interpret the thesis?
We can get some tips from the Apollonian ideal. Prominent in that is the intellectual virtue of clarity, intelligibility, theoretical power -- rational virtues belonging to systems of ideas, and to the key elements of such systems. Thus one can say that the golden section is a beautiful ratio and that the parabola is one of the many beautiful products of that ratio. Similarly one can speak of elegant proofs, ones that succeed in proving a theorem less ploddingly and more imaginatively, in fewer steps than their inelegant counterparts. These virtues have traditionally been called intellectual beauties because they are the goal of the intellect, which best appreciates them.
It seems likely that Plato would have wanted to explain the beauty of Beauty in these terms had he ever given enough attention to the question. For what other basis could be found for admiring abstractions aesthetically, as beauties? Once one has seen clearly that the beauty of Beauty is not its mere self-identity, there seems nothing else left but the appeal to the intellect.
However, it is not at all clear that such a justification will work. For if one compares Beauty -- the Form, property, or (if it helps) the concept or idea -- with the classic abstract beauties of mathematics and other domains, it seems most implausible to think it is even as beautiful as they, let alone supremely beautiful. For it is not easy to define. It defies clear understanding. It has not been shown to be theoretically powerful in giving intelligible structure to the domain of aesthetics, in explaining our aesthetic experience in a comprehensive, specific and satisfying way. That is not to say it doesn't exist, but only that it doesn't seem particularly beautiful in the intellectual way. It doesn't seem elegant or neat. For all we can tell (and for all Plato tells us) it may be somewhat messy, complicated, vague.
If it turns out not to be beautiful, I hasten to add, Plato's theory does not collapse. The claim that beauty is self-exemplifying can be deleted from his theory without jeopardizing any of the rest. We should then put this part of his theory on one side, as a nonessential, even though this decision might shock Plato. Item v on our list must be amended by putting brackets around the last clause. Perhaps beauty is not maximally beautiful, or even not beautiful at all.
32
Do i-vii as amended suffice to identify beauty? The answer is yes if nothing but beauty can satisfy them and if every sort of beauty is captured by them.
As to the first, do such closely related Forms as justice, courage and other moral virtues satisfy i-vii? No, they do not satisfy iii, according to Plato, at least. That principle places emphasis on the sensory connection of beauty. But Plato has Socrates say in the Phaedrus excerpt that to see their sensible instances is not typically to love them. And perhaps he would add that even when we understand them, grasp their justice or courage, their degrees do not typically bring corresponding pleasure. This seems plausible, since strict justice may be harsh and forbidding, and kindness may be great without being graceful or insightful. Perhaps the same can be said for all other comparative properties. (Obviously an extensive inquiry would be necessary to verify this.)
But what about the second? Does Plato's Apollonian beauty capture the full range of beauty? Not obviously. For it frowns on Dionysian values, which seem to have just as much claim to being aesthetic (rather than moral, intellectual, utilitarian, etc.). Are these to be counted as lesser beauties, somewhere lower on the beauty scale? Are they even forms of ugliness? Or may they (some of them, anyway) also be beautiful?
The problem is not an easy one, and Plato's writings offer us few leads. It's something we must pursue largely on our own.
There is also another serious problem for Plato's theory. We have already discussed the problematic item vi, the unitariness of beauty. There may simply be no response-independent property which is the same in all the kinds of beauty accepted as such by Plato. Bodily beauty may not have enough in common with intellectual beauty to be explained in terms of a single inherent property. They may not even be able to be placed on the same scale. If this is so, a fundamental part of Plato's theory has to be given up, one so fundamental as to call the whole in question.
The natural way to respond to this threat is by giving up the requirement of inherence, substituting for it the idea of a percipient-relational property, for instance, the property of being aesthetically pleasing in some way which preserves the basic objectivity of beauty. But that option is strongly anti-Platonic. Plato wants beauty to be loved because it is beautiful, not beautiful because it is loved. Inherence (response-independence) is essential to the cherished autonomy of beauty.
The consequence of all this is that we cannot be sure that any amendment of i-vii acceptable to Plato has a Form which satisfies those conditions. Thus even if he is right about the nature of the Forms and about beauty being a Form, he may be deeply wrong about which Form it is and even to which general category of Forms it belongs. His specific ontology may be wrong. And the problem seems insoluble to almost all philosophers today: there is no plausible candidate for a response-independent property of beauty.
However dubious Plato'sontology may be, other parts of his theory, specifically his epistemology of beauty may be on the right track. And if it's not, we must find out how and why. To that final topic we now turn.
33
9. Plato's epistemology concerning beauty
Epistemology, or theory of knowledge, concerns the concepts of knowing, having reason to believe, and so forth. As already indicated, Platonists hold that there are two sharply different sorts of knowledge, a priori and a posteriori (or empirical) knowledge. (Plato did not use these terms which came later, but the distinction is the same.) Plato himself usually called only the first knowledge, using the term belief or opinion for the empirical sort. Present day usage is less restrictive with the term knowledge, relying on the qualifiers to make the distinction. Thus for us Plato's view of knowledge of beauty is expressed by saying that some things we know a priori and others we know empirically (a posteriori). When we are dealing with ideals, or principles, we may, on Plato's view, attain a priori knowledge, though of course we often fall short. When we deal with particular cases (concrete particulars) a priori knowledge is beyond reach, Plato believes. At best empirical or a posteriori knowledge is possible. In both cases, according to current usage, the difference between knowledge and (mere) belief or opinion is a matter of the strength of the grounds on which our belief is based.
The model for a priori knowledge is mathematics, though there are other good examples as well. In mathematics we have knowledge based on self-evident axioms (at least according to Platonists we do) and their demonstrable theorems. If our minds are clear and our mental powers fully exerted, we seem capable of insight so potent it couldn't be wrong. How far such premium-grade cognition extends is a matter of great variation person to person and moment to moment. Even clever people can commit mathematical blunders. But the collective brain power of centuries has put much mathematics beyond the reach of reasonable doubt.
This is the positive side of the argument for the superiority of a priori knowledge. The other side is that empirical evidence, that is, evidence drawn from sensory observation, however strong, cannot provide rational certainty of the same degree. The possibility of deception by our senses seems impossible to rule out to the same extent as it is in purely conceptual cognition. This generalization is reinforced by the fact that such evidence doesn't apply to pure mathematics and other fields in which premium-grade certainty is attainable. One cannot verify any mathematical proposition by empirical observation or measurement. The reason is that any discrepancy between pure mathematics and measurement is always more reasonable to resolve by discounting the measurement and keeping the mathematics. So if we discover that our surveying instruments triangulating space from three mountain peaks come up with 180.00001° as the sum of the internal angles, we will more reasonably explain this by saying that either the instuments are inaccurate (or the use of them is) or else light does not travel in precisely straight lines than by saying that a Euclidean triangle's interior angles do not sum to precisely 180°. Similarly for arithmetical truths, when we find that volumes of liquids and gases do not combine in simple sums of the constituent volumes.
This is all very well for mathematics, you may think, but what reason is there for thinking that beauty is knowable in that (a priori) way? A Platonic answer would begin by claiming that beauty, like mathematical abstracts, can be clearly conceived as an abstract ideal. This means that at least some propositions about beauty are self-evident or demonstrable by deduction from self-evident starting points. It will not claim, nor does it need to, that any of these propositions are as easily known as the simplest mathematical truths. Well, one may inject, let's have some of these truths. Plato, let's imagine, produces such examples as this: other things being equal, rational states of mind are more beautiful than irrational ones (he never says anything exactly like this but what he does say makes this a reasonable candidate). Or he may proceed by cases: imagine a temple like the Parthenon, made geometrically correct (eliminate the optical and other deviations), regarded not from a perceptual point of view but in a purely conceptual way, as an architect might think of it in his mind's eye. Compare this with the same form distorted by conspicuous sagging, seeing if you can avoid transforming it into some redeemingly comic or dynamic form -- for instance these examples: (See Beauty Supplement p. 95 for better examples and a quiz to test your sensitivity to the distortions.)
34

You should not have much difficulty convincing yourself that the regular temple is self-evidently more beautiful than the sagging or cockeyed one. (The case can easily be made for pots, too.) Just as in mathematics it seems that anyone who seriously disagreed could not possibly grasp what beauty is. When they say the first is just as beautiful as the second, or worse, more beautiful than it, they must be confused in something of the way in which a person is who insists that 2 + 3 = 6. They must not be focusing their mind sharply enough (perhaps they are confusing addition with multiplication), or must be under the domination of some delusion (e.g. a paranoid delusion of having been subjected to demonic possession which makes them add one digit short, so that they must always add one to obtain the correct value). What specific confusion or dysfunction they suffer would have to be elicited by further examination, but there must be some such explanation.
In such cases Platonists argue that no empirical finding could possibly undermine our reasonable conviction. That some people, as a result of psychological trauma, find geometric regularity oppressive will not be relevant precisely because the response is defective. And it is hard to imagine any aesthetic reason for favoring geometrical irregularity of the unredeemed sort displayed in the example. Nor will it matter whether nature does or doesn't produce (many) geometrically regular objects. For we must judge nature by aesthetic standards, not judge our aesthetic standards by reference to it.
Admittedly such truths are just a beginning. But they do suggest that beauty has a stronger claim to objectivity based on a priori principles than many people believe nowadays. A complete case for Plato's view would require developing a comprehensive set of beauty-principles, just as a complete case for the objectivity of mathematics requires the same thing for its field. In the course of such developments lots of brainy, motivated people expend enormous energy on the subject, and collectively the effort bears fruit. In beauty as in mathematics and geometry nothing but success can establish the reality of a priori truths.
35
But, you may say, so far the collective result of study of beauty has yielded lots and lots of disagreement! Individuals and cultures notoriously disagree about beauty. How, then, could we have reason to think it possible to work our way toward a consensus about a whole system of beauty?
The only defence against this challenge is the observation that there are plenty of reasons for thinking that a vast amount of the disagreement is founded on narrow-mindedness and negligence. People have powerful motives to perpetuate disagreements. But these are not entirely creditable motives, even if sometimes they are excusable. They generally stem from the desire to think ourselves superior to others (therefore holding fast to the superiority of our traditional values) or to a kind of cowardice that keeps us from asserting ourselves if it makes others uncomfortable, or to the desire to go on enjoying ourselves without bothering to understand the tastes of others. And if so much disagreement is rooted in such sources, it may be that with a clearer and more comprehensive view of things, and a purer motivation, people would find themselves moving toward greater agreement for the right reasons.
A few paragraphs back I said that on Plato's view knowledge of the beauty of concrete particulars is at best empirical. The reason is this. The proposition that a particular building or painting or person is beautiful inevitably breaks down into two propositions, first that the individual has some shape, color, or other properties of the non-aesthetic sort (ones which are not themselves value properties), the second that these properties make the individual beautiful. At least this is how a Platonist views the matter. Thus such claims involve both an empirical recognition of physical or mental qualities in the concrete particular and the assertion of a beauty-principle to the effect that anything which has those properties is beautiful. They say, in effect, this thing has such-and-such properties which, in virtue of the principle, make it beautiful. So even if the principle is knowable a priori, the other part of the claim (that the thing has such-and-such properties) is empirical, and thus the claim as a whole depends upon sensory observation, which is what it means to call it empirical.
Because claims about the beauty of concrete particulars can never have the immunity to empirical disconfirmation that is enjoyed by a priori truths, it is not surprising that Plato assigns them a lesser status than beauty-principles.
Still, there is no reason for a modern Platonist to deny that knowledge of
the beauty of particulars can be as well-founded as knowledge of beauty-principles,
since the empirical part of our judgments can be beyond reasonable doubt --
and in fact much better founded than many of our speculations about principles
of beauty.
Equally, the Platonist can agree that for practical purposes it is often reasonable
to accept a priori principles of beauty on the authority of another rather
than from one's own direct insight, even though reliance on authority rests
on empirical grounds -- specifically that the authority holds a respected position
in the relevant part of society. Though reliance on authority is never the
best ground of belief, it is often the best ground available to us in the circumstances.
Our reliance on authorities in higher mathematics is an obvious case in point.
The result is that we must not overstress the a priori element in a properly Platonic theory of knowledge of beauty.
36
Parting shot: a deep difficulty
Well, you may think to yourself, this doesn't leave me with a very definite idea of aesthetic knowledge. Making such knowledge like mathematical knowledge seems fraudulent because in mathematics we begin with axioms and definitions and then draw the consequences. But Plato hasn't given us any sharply formulated axioms or definitions. And if we took such a principle as rationality being more beautiful than irrationality for an axiom, it still seems that the experience of testing it in one's mind is different from anything that goes on in mathematics. It seems necessary to use something more than a purely intellectual approach. We seem to have to appreciate the object aesthetically, not just understand it intellectually.
This complaint has been made by philosophers, too. With some realms of beauty the difficulty seems particularly acute. The beauty of color, tone, smell, taste, etc. seem to be accessible to us only through sensory experience. As Kant was to say, we insist upon submitting the allegedly beautiful thing to our senses to see for ourselves whether it is beautiful. If someone's theory dictates that it must be beautiful, whether or not direct inspection bears out this claim, we rightly suspect the theory. And we are reminded here of what Plato himself said in the Phaedrus about beauty differing from wisdom and other values in that it alone is accessible to us via our senses. The a priori conception of knowledge of beauty does not seem entirely to square with this idea. Aesthetic intuition, we might say, seems more particularistic than universalistic.
In this respect beauty can be interestingly contrasted with moral goodness. For we seem able adequately to conceive of moral goodness in the absence of a concrete case before us. Direct sensory experience or immediate feeling seems not to be essential, or at least not as essential as it is in the case of beauty. So it may be that even if normative criteria of beauty are universal and necessary, like ordinary a priori truths, they are knowable only on the basis of direct experience, whether perceptual or conceptual.
We might put it this way: the sensory connection (more properly the immediate experience connection) may cut deeper than it seemed. It may be as important as the mathematical connection.
Without supposing that we have gotten to the bottom of the big questions raised by Plato's theory of beauty (or that he did either), we must move on to other theories.
37
Plato's theory of beauty in historical context
Of the Greek 4th century B.C. writings concerning beauty which have survived the wreck of history, Plato's are by far the fullest and best developed. Yet Plato's views on beauty were by no means universally accepted. Probably they did not represent a majority opinion among the Greek intelligentsia of his day. The idea of Forms was viewed with suspicion even by some of Plato's close associates. As to beauty in particular, probably as many persons inclined to the scepticism of the Sophists as to Plato's idealism. The Sophists, teachers of the skills needed in the assembly and law courts, typically espoused the view that there is no objective beauty just as they contended that there is no entirely objective truth about anything. There is only pleasure/displeasure in the case of beauty and opinion in the case of "truth." Beauty for one person need not bear any relation to beauty for another, and similarly with truth.
At least that is what the two most famous Sophists are reported to have asserted. Gorgias and Protagoras are said to have held radical forms of subjectivism. It is impossible to know how seriously they held these views. To some extent they may have adopted them to show their skill in argument. If they could make these claims convincing, they could perhaps teach a pupil how to win any case. Further, Protagoras is reported to have said that while truth is reducible to mere opinion, it matters a lot which opinion a person adopts: some "truths" are more useful than others. But this criterion of usefulness looks like residual objectivity. If we have to accept truths about usefulness how can he justify believing that other sorts of truth don't exist? Consistent, universal subjectivism was as fraught with difficulties in classical Athens as it is today.
Whether or not Plato's ideas were popular during his day, they were indisputably of immense importance in subsequent Western thought about beauty. His most famous pupil, Aristotle, reinforced his master's reputation by frequent references to him. While dissenting on important points, his philosophy was indelibly marked by his inheritance from Plato. The same can be said for countless other thinkers. Plato had founded a school, the Academy, which existed without interruption for nine hundred years. His writings were preserved and diligently studied throughout this long period. The Academy remained a major fixture in Athens, which survived as a center of culture for most of the Graeco-Roman period, long after Greece had been absorbed into the Roman Empire. Educated Romans had great reverence for Greek learning and above all for the classics of the 4th century. After the center of power was shifted from Rome to Constantinople (shortly to become Byzantium) court intellectuals kept the memory of Plato very much alive, as did Christian thinkers in the West, like Augustine, whose theology is a fusion of Platonism and Judaism. Greek thought suffered comparative oblivion in the early Middle Ages but by the end of the 15th century Plato's dialogues had been rediscovered, translated and used as sources of wisdom. The story continues through the 19th century with such thinkers as Schopenhauer giving a new interpretation of Platonism in a context of Romanticism; and it extends even into the 20th century in analytic philosophy, in the work of Bertrand Russell, and phenomenology, in the thought of Edmund Husserl and others. Of course these thinkers don't accept Plato whole. They take key ideas and weave them together with entirely new elements, in recognition of the problems that Plato never solved. Plato's basic theory thus provided enduring inspiration for various forms of realism concerning abstractions, both in metaphysics and value theory. And his works continued to be mined for insights and conjectures about these subjects.
38
The following excerpts present some of the most notable contributions to the classical and medieval tradition springing from Plato. Aristotle's realism is an important variation on Plato's. The difference here may appeal to some of you who find the Forms a big problem. Plotinus' revival of Platonism (called neo-platonism) is essentially a continuation of Plato's thought carried in a more mystical direction, one that spawned a robust strain of mysticism in Christian theology. St. Thomas, the great scholastic theologian, represents a continuation of Aristotle's dissent from Plato concerning beauty. Through their thought runs an unresolved ambivalence about the status of beauty which sets the scene for the next major type of aesthetic theory, the 18th century sense of beauty conception of beauty.
Aristotle on beauty and artistic value
In spite of his remarkably encyclopedic writings, Aristotle gives us little on beauty. His major contribution to aesthetics consists of an extended discussion of tragedy in the Poetics. Another work, On Poets, is lost. From the Poetics we learn much about criteria of excellence for tragedies, but it is difficult to project anything much about beauty in general from this, since beauty is not necessarily the only or even the main consideration in evaluating tragedy. In the Nichomachean Ethics Aristotle tells us a lot about the good and the pleasant, but once again it is risky to impute to Aristotle himself very much from this about the beautiful if one wants to be strictly scholarly about it. Still, in time a medieval tradition grew up based on inferences drawn from things Aristotle says about beauty in scattered passages, and there is no reason not to take cognizance of this and call it Aristotelian. (In fact it is an ancestor of the sort of reconstruction of historical theories which I practice in this text, so there is special reason for me to acknowledge it.) In this spirit I present the following collection of brief passages. In them are found a number of seminal ideas mingled with revealing ambiguities and contrary tendencies. Generously interpreted the totality suggests interesting lines for development but no single, consistent theory.
4. Aristotle's ontology of beauty
We may begin with an inference from one of Aristotle's criticisms of Plato: if Aristotle believed there was a single property of beauty (which is not certain), he did not believe that it existed in complete separation from its exemplifications. In many passages he makes quite clear that he believes universals (properties) exist only in their exemplifications. Rather than being transcendent they are immanent in the world. However, we must not restrict exemplifications to material particulars, since on Aristotle's view thought by itself effects a kind of exemplification. The full, well-formed thought of a property gives the property a mental instantiation: the property of which I am thinking (e.g., triangularity) is actually present in my mind. So ideals such as beauty or justice are existent when adequately conceived. Further, Aristotle also believes in a divine mind (the Unmoved Mover) who seems eternally to contemplate all things universal -- for such contemplation, he believes, is the most divine sort of activity. So universals (properties, essences) always exist in the divine mind. Such eternity is at least a close cousin of Plato's.
39
Here are some of the scattered passages in which Aristotle says things bearing on the ontology of beauty. Scrutinize them for suggestions concerning the ontology of beauty. You should find conflicting tendencies in them. Some suggest that beauty is autonomous with respect to its effect on us, some that it is essentially related to human capacities.
Now since the good (1) and the beautiful are different (for the former always implies conduct as its subject, while the beautiful is found also in motionless things), those who assert that the mathematical sciences say nothing about the beautiful or the good are in error. For these sciences say and prove a great deal about them; if they do not expressly mention them, but prove attributes which are their results or their definitions, it is not true to say that they tell us nothing about them. The chief forms of beauty are order and symmetry and definiteness, which the mathematical sciences demonstrate in a special degree. And since these (e.g. order and definiteness) are obviously causes of many things, evidently these sciences must treat this sort of causative principle also (i.e. the beautiful) as in some sense a cause. (2) But we shall speak more plainly elsewhere about these matters. (Metaphysics XIII, 1078a33).
[Trans. W.D. Ross. 1. good = moral/ethical good, apparently. What about the functional good of a tool? This criterion doesn't draw a line between that and beauty. 2. Cause is used here in a wide technical sense embracing the goal of processes.]
Since every sense is active in relation to its object, and a sense which is in good condition acts perfectly in relation to the most beautiful of its objects..., it follows that in the case of each sense the best activity is that of the best conditioned organ in relation to the finest of its objects. (3) And this activity will be the most complete and pleasant. For, while there is pleasure in respect of any sense, and in respect of thought and contemplation no less, the most complete is pleasantest, and that of a well-conditioned organ in relation to the worthiest of its objects is the most complete; and the pleasure completes the activity. ( Nicomachean Ethics X, 1174b15)
... in painting... the most beautiful colors laid on without order will not give one the same pleasure as a simple black-and-white sketch of a portrait. (Poetics 1450b1)
[ 3. An emphatically cognitive criterion of visual beauty: the (visually) most beautiful object is the one that most completely exercises the best eye. Similarly for the other sense-modalities.]
... to be beautiful, a living creature, and every whole made up of parts, must not only present a certain order in its arrangement of parts, but also be of a certain definite magnitude. Beauty is a matter of size and order, and therefore impossible either (1) in a very minute creature, since our perception becomes indistinct as it approaches instantaneity; or (2) in a creature of vast size-one, say 1,000 miles long -- as in that case, instead of the object being seen all at once, the unity and wholeness of it is lost to the beholder. (4) (Poetics 1450b34)
[4. In the Poetics Aristotle uses a criterion of organic unity, where every part is necessary. Any loss or alteration is then for the worse.]
40
Taking some liberties with Aristotle's texts, in line with the practice of later Aristotelians, we can build some reasonable conjectures about what Aristotle would have said about beauty if he had dealt with it systematically. For instance, from his emphasis on organic unity as a prime criterion of good drama and from his statement that in general art completes or improves upon nature, we may infer that for him things will be more beautiful in proportion as they attain a high degree of harmonious development of the potentialities of their species or type. On this basis the most beautiful member of a species is the one most fully realizing the essential traits of the species. The most beautiful horse is the one realizing most fully the essential equine traits, and the same for an iguana.
Similarly it is tempting to think that when Aristotle speaks of some things being good abstractly, for instance those things that satisfy reason, he would also be willing to say that these were most beautiful. This would give us a criterion of beauty transcending particular species. Thus when Aristotle says that the best motion is unvarying motion in a circle, or what is best is what gives enjoyment to the most rational being, it is not unreasonable to think that he might have said that these things were also the most beautiful. We can thereby derive parts of a normative aesthetic which are not unreasonable to dub Aristotelian. For a practical application of this Aristotelian aesthetic, see Judith Forbis' analysis of the virtues and defects of Arabian horses, to be posted later. This case would have appealed to the upper-class Athenian public for which Plato and Aristotle wrote.
2. Aristotle's epistemology of beauty
From Aristotle's theory of knowledge we can also extract plausible epistemological principles relating to beauty. Taking our departure from what Aristotle says about ethical values and about knowledge and reality generally, we can formulate at least rudiments of an epistemology of beauty.
One thing is sure. Aristotle's theory commits him to a priori knowledge of aesthetic principles corresponding to knowledge of ethical principles -- normative criteria of beauty (or in ethics, of goodness, duty, etc.). However, Aristotle is plainly opposed to Plato concerning principles of beauty. First, they are not as systematic and certain as are the truths comprising geometry or mathematics. Aristotle explicitly recognizes the greater degree of imprecision in matters of value. So he could not consistently aspire to a finished system of aesthetic principles. Plato, as I have represented him, does aspire to such a system -- that is, a complete body of aesthetic principles adequate to produce a master ranking of all beauty. For Plato, only human limitations keep us from success in this endeavor.
Second, Aristotle's general epistemology implies that a priori knowledge has a greater psychological dependency on perception than Plato thinks it does. We can form an adequate conception of an essence (Aristotle's term for his non-transcendent abstract objects, like Plato's Forms except for not existing separately from their exemplifications) only on the basis of intensive scrutiny of the instances. And in the case of essences of natural species or artifacts or mental or moral qualities this requires perceptual or introspective scrutiny of the particulars. The essence seems to emerge into full clarity only from intimate knowledge of things in the world of space and time. Though achieved knowledge of the essence is a priori, that is, cannot be verified by empirical experiments but only by pure intellection, still the intellectual processes must take full account of actual and possible perceptual or introspective experience of particulars. In short, after immersion in particulars, the intellect is in a position to know the essence, but not until then. Premature theorizing about essences is idle.
41
In this insistence on thorough acquaintance with particulars, Aristotle differs in degree from Plato, whose general epistemological stragegy is to rise above the world of particulars as soon as possible, Immersion in the world of space and time -- e.g. in the details of anatomy or of nutrition and propagation of a species, is more apt in his view to obscure the true character of the Form of the species. To be sure, Plato is not altogether neglectful of the practical necessity of our working toward a priori knowledge from empirical experience, but the difference of degree is important.
Applying this difference to knowledge of beauty, we get the following. Aesthetic principles will be knowable, for Aristotle, only on the basis of intensive aesthetic experience of the instances to which the principles apply. In the case of concrete particulars, one must know intimately the look and feel of the instances -- say, of visual designs or musical forms -- before generalizing about symmetry, proportionality, balance, harmony, etc. Further, it is reasonable to infer that for Aristotle the securest a priori knowledge is knowledge of fairly specific principles: principles relating to fairly narrow types of things -- to visual designs or musical forms or architectural masses or dramatic forms, rather than to all things in general. This would accord with his criticisms of Platonists' belief in a single Form of Goodness. Aristotle argues that good has different senses when applied to different categories, and therefore there is no one Idea of the good-itself. I believe it follows that for him there can be no one rank ordering of goodness on which everything can be precisely placed, and it seems highly plausible he would hold the same view of beauty.
Between Aristotle and Plotinus
During the 500 years between Aristotle and Plotinus intellectual life was vigorous and thinkers certainly discussed beauty. But very little is left, especially of Hellenistic writings about beauty. One major idea appearing in this period may be identified from later sources, namely the idea of the phantasia in the mind of the artist or appreciator of beauty. The great Roman orator Cicero presents this notion in the following passage, written in the first century B.C.
...I am firmly of the opinion that nothing of any kind is so beautiful as not to be excelled in beauty by that of which it is a copy, as a mask is a copy of a face. This ideal cannot be perceived by the eye or ear, nor by any of the senses, but we can nevertheless grasp it by the mind and the imagination. For example, in the case of the statues of Phidias, the most perfect of their kind that we have ever seen, and in the case of the paintings I have mentioned, we can, in spite of their beauty, imagine something more beautiful. Surely that great sculptor, while making the image of Jupiter or Minerva, did not look at any person whom he was using as a model, but in his own mind there dwelt a surpassing vision of beauty; at this he gazed and all intent on this he guided his artist's hand to produce the likeness of the god. Accordingly, as there is something perfect and surpassing in the case of sculpture and painting-an intellectual ideal by reference to which the artist represents those objects which do not appear to the eye [for instance, gods and perhaps other mythological personages ], so with our minds we conceive the ideal of perfect eloquence (Cicero's subject is rhetoric], but with our ears we catch only the copy. These patterns of things are called ideai [Ideas, Forms] by Plato, that eminent master and teacher both of style and of thought... (Orator III, 8-10)
Cicero makes a connection here between beauty and representational art that Plato evidently did not, judging from the Book X of the Republic. This connection was to become the cornerstone of artistic theory in the Renaissance.
42
Plotinus' theory of beauty
Plotinus (204-69 A.D.) revived and modified Plato's philosophy, considerably
increasing the mystical element in it. His writings were collected by his pupil,
Porphyry, and arranged in six Enneads (literally, of nine parts each).
As background, let me first sketch Plotinus' cosmology or theory of reality
at large, even though I can give only the roughest sketch of it. Plotinus conceived
of all reality as the outflowing of a single mystical being, "the one",
which was ineffable (literally indescribable) and capable of being apprehended
only in exalted mystical states of consciousness. The "emanations"
of this One formed a continuous hierarchy of beings: Divine Intellect, the Platonic
Forms, the World Soul, individual souls, physical things ranging from the most
refined to the grossest, and at the bottom raw matter. This ordered array of
things filled all possible grades of being, and came to be known as the Great
Chain of Being. The philosopher's quest is to rise up as far as possible in
the chain of being by developing the aspects of himself that stand highest in
it, which are of course his intellectual and moral capacities, as Plato says
in the Symposium. This ascent achieves as much beauty as we are capable of;
above our reach stand yet more beautiful beings which we can only contemplate.
Plotinus' texts give us more about beauty than any of those which have survived
other than Plato's. Further, he is the first thinker to write an extended essay
specifically on beauty. The following sections present some of the more notable
parts of his discusssions.
As mystical as Plotinus is, at times he becomes rigorously analytical, as in this argument against the view that beauty being the reducible to symmetry of parts and charm of color. (trans. S. Mackenna)
What is it that attracts the eyes of those to whom a beautiful object is presented, and calls them, lures them, toward it, and fills them with joy at the sight? If we possess ourselves of this, we have at once a standpoint for the wider survey.
Almost everyone declares that the symmetry of parts towards each other and towards a whole, with, besides, a certain charm of colour, constitutes the beauty recognized by the eye, that in visible things, as indeed in all else, universally, the beautiful thing is essentially symmetrical, patterned.
But think what this means. [On such a hypothesis] only a compound could be beautiful, never anything devoid of parts, and only a whole; the several parts would have beauty not in themselves but only as working together to give a comely totality. Yet in fact [contrary to the hypothesis] beauty in any aggregate demands beauty in details; it cannot be constructed out of ugliness; its law must run throughout.1
All the loveliness of colour and even the light of the sun, being devoid of parts (2) and so not beautiful by symmetry, must [on the hypothesis] be ruled out of the realm of beauty. And how [on that theory] comes gold to be a beautiful thing? And lightning by night, and the stars, why [according to the theory] are these so fair?
[1. Here Plotinus repeats the idea in Plato's Symposium that really beautiful things must be beautiful through and through. But it is highly dubious, since its suggests e.g. that sculptures are more beautiful if made of precious materials. 2. It is not easy to know whether light, color, and musical tones should be regarded as simple or complex in their aesthetic aspect, that is, as they are experienced. Can we perceive any complexity in them? Plotinus thinks not, but we can certainly distinguish hue from brightness and saturation, and pitch from loudness and tone quality. However, Plotinus' main point does not require the strict simplicity of these things, but only that there be no parts which could be symmetrically arrayed. And that seems undeniable. His argument could easily be recast to avoid the problem of strict simplicity.]
43
In sounds also the simple must be proscribed though often [contrary to the hypothesis] in a noble composition each individual tone is delicious in itself.
Again since the one face, constant in symmetry, appears sometimes fair and sometimes not, can we doubt that beauty is something more than symmetry, that symmetry itself owes its beauty to a remoter principle?
Turn to what is attractive in methods of life or in the expression of thought; are we to call in symmetry here? What symmetry is to be found in noble conduct, or excellent laws, in any form of mental pursuit?
In sounds also the simple must be proscribed though often [contrary to the hypothesis] in a noble composition each individual tone is delicious in itself. What symmetry can there be in points of abstract thought?
The symmetry of being accordant with each other? But there may be accordance or entire identity where there is nothing but ugliness; the proposition that honesty is merely a generous artlessness chimes in the more perfect harmony with the proposition that morality means weakness of will; the accordance is complete.
Then again, all the virtues are a beauty of the soul, a beauty authentic beyond any of these others; but how does symmetry enter here? The soul, it is true, is not a simple unity, but still its virtue cannot have the symmetry of size or of number: what standard of measurement could preside over the compromise or the coalescence of the soul's faculties or purposes?
Finally, how by this theory would there be beauty in the Intellectual-Principle, essentially the solitary? (Ennead I, 6, §1)
Like Plato, Plotinus stresses how spontaneous our response to beauty and ugliness is:
...it is something perceived at first glance, something which the soul names as if from an ancient knowledge and, recognizing it, welcomes it, even enters into unison with it.
But let the soul fall in with the ugly and at once it shrinks within itself, denies the thing, turns away from it, not accordant, resenting it.
Our interpretation is that the soul -- by the very truth of its nature, by its affiliation to the noblest Existents in the hierarchy of Being -- when it sees anything of that kinship, thrills with an immediate delight, (3) takes its own to itself, and thus stirs anew to the sense of its nature and of all its affinity. Ennead, I, 6, 2.
[3. Plotinus gives the impression that the delight never fails, as if beauty always thrills. But elsewhere he acknowledges that this holds only for the purified soul. Commonly people fall short of this ideal because they are in some degree corrupt or ill-trained. The term immediate in this context is mainly a matter of the delight not depending on our ability to explain what is so good about the thing that delights us.]
44
The following excerpts reflect the Apollonian ideal and were more influential in the Middle Ages than were Plato's writings, which were less widely available than were those of Plotinus and Christian Neoplatonists.
We hold that all the loveliness of this world comes by communion in Ideal-Form.
All shapelessness whose kind admits of pattern and form, as long as it remains outside of Reason and Idea, is ugly by that very isolation from the 'Divine-Thought. And this is the Absolute Ugly: an ugly thing is something that has not been entirely mastered by pattern, that is by Reason, the Matter not yielding at all points and all respects to Ideal-Form.
But where the Ideal-Form has entered, it has grouped and coordinated what from a diversity of parts was to become a unity; it has rallied confusion into cooperation; it has made the sum one harmonious coherence; for the Idea is a unity and what it moulds must come to unity as far as multiplicity may.
And on what has thus been compacted to unity, Beauty enthrones itself, giving itself to the parts as to the sum: when it lights on some natural unity, a thing of like parts, then it gives itself to that whole. Thus, for an illustration, there is the beauty, conferred by craftsmanship, of all a house with all its parts, and the beauty which some natural quality may give to a single stone. (§2)
The beauty of color is also the outcome of a unification: it derives from shape (1), from the conquest of the darkness inherent in Matter by the pouring-in of light, the unembodied, which is a Rational-Principle and an Ideal-Form.
Hence it is that Fire itself is splendid beyond all material bodies, holding the rank of Ideal Principle to the other elements, making ever upwards, the subtlest and sprightliest of all bodies, as very near to the unembodied; itself alone admitting no other, all the others penetrated by it; for they take warmth but this is never cold; it has colour primally; they receive the Form of colour from it: hence the splendour of its light, the spendour that belongs to the Idea. And all that has resisted and is but uncertainly held by its light remains outside of beauty as not having absorbed the plentitude of the Form of colour.
And harmonies unheard in sound create the harmonies we hear (2) and wake the Soul to the consciousness of beauty, showing it the one essence in another kind: for the measures of our sensible music are not arbitrary but are determined by the Principle whose labour is to dominate Matter and bring pattern into being.
Thus far of the beauties of the realm of sense, images and shadow-pictures, fugitives that have entered into Matter -- to adorm, and to ravish, where they are seen. (Ennead I, 6, §3)
[1. It is hard to make out what Plotinus could mean by color being derived from shape. Perhaps it is connected with the idea of color being a mixture of daylight and darkness derived from matter. He seems to believe that color results from daylight being partly absorbed by the matter of things which we see as colored, and the shape of the particles of matter may produce the different mixtures we see as color. 2. The unheard harmonies are the pure mathematical ratios involved in musical harmony. Plotinus thinks that the soul responds to the mathematics rather than to the heard qualities of sound]
45
Plotinus picks up the phantasia idea earlier expressed by Cicero and in addition neatly inverts Plato's argument about the mimetic arts. They can't be much worse than natural objects if they are so much like them. Further, he develops Aristotle's idea that artists (in the broad sense which includes craftsmen) create as nature does. They don't merely produce imitations of nature's products. So conceived the best artist is just one step below the creative principle in nature, which is a compliment, coming from someone so finely tuned to the glories of the world as Plotinus. This last is demonstrated by praise of nature in the same passage, even though here and elsewhere he stresses the incomparable beauty of purely spiritual things, from individual souls all the way up to the One, or Intellectual-Principle, which is beyond mere beauty.
Still the arts are not to be slighted on the ground that they create by imitations of natural objects; for, to begin with, these natural objects are themselves imitations; then, we must recognize that they give no bare reproduction of the thing seen but go back to the Reason-Principles from which Nature itself derives, and, furthermore, that much of their work is all their own; they are holders of beauty and add where nature is lacking. Thus Pheidias wrought the Zeus upon no model among things of sense but by apprehending what form Zeus must take if he chose to become manifest to sight. (Ennead V, 8, §1)
Whence shone forth the beauty of Helen, battlesought; or of all those women like in loveliness to Aphrodite; or of Aphrodite herself; or of any human being that has been perfect in beauty; or of any of these gods manifest to sight, or unseen but carrying what would be beauty if we saw?
In all these is it not the Idea, something of that realm but communicated to the produced from within the producer, just as in the works of art, we held, it is communicated from the arts to their creations? Now we can surely not believe that, while the made thing and the Idea thus impressed upon Matter are beautiful, yet the Idea not so alloyed but resting still with the creator -- the Idea primal, immaterial, firmly a unity -- is not Beauty. (§2)And indeed if the divine did not exist, the transcendently beautiful, in a beauty beyond all thought, what could be lovelier than the things we see? Certainly no reproach can rightly be brought against this world save only it is not That. (§8)
In the next passage Plotinus speaks about the process of inner reflection which he believes is required if we are to refine and deepen our apprehension of beauty. It provides a corrective to any hasty conclusion from the earlier reference to our knowledge of beauty as immediate and spontaneous. "We must close our eyes and invoke a new manner of seeing, a wakefulness that is the birthright of us all, though few put it to use." He continues:
46
What, then, is this inner vision?
Like anyone just wakened, the soul cannot look at bright object. It must be persuaded first to look at beautiful habits, then the works of beauty produced not by craftsman's skill but by virtue of men known for their goodness, then the soul of those who achieve beautiful deeds. "How can one see the beauty of a good soul?" Withdraw into yourself and look. If you do not as yet see beauty within you, do as does the sculptor of a statue that is to be beautified; he cuts away here, he smooths it there, he makes this line lighter, this other one purer, until he disengages beautiful lineaments in the marble. Do you this, too. Cut away all that is excessive, straighten all that is crooked, bring light to all that is overcast, labor to make all one radiance of beauty. Never cease "working at the statue" until there shines out upon you from it the divine sheen of virtue, until you see perfect "goodness firmly established in stainless shrine." Have you become like this? Do you see yourself, abiding within yourself, in pure solitude? Does nothing remain now to shatter that interior unity, nor anything external cling to your authentic self? Are you entirely that sole true light which is not contained by space, not confined to any circumscribed form, not diffused as something without a limit, but ever unmeasurable as something greater than all measure and something more than all quantity? Do you see yourself in this state? Then you have become vision itself. Be of good cheer. Remaining here you have ascended aloft. You need a guide no longer. Strain and see.
Only the mind's eye can contemplate this mightly beauty, But if it comes to contemplation purblind with vice, impure, weak, without the strength to look upon brilliant objects, it then sees nothing even if it is placed in the presence of an object that can be seen. For the eye must be adapted to what is to be seen, have some likeness to it, if it would give itself to contemplation. No eye that has not become like unto the sun will ever look upon the sun; nor will any that is not beautiful look upon the beautiful. Let each one therefore become godlike and beautiful who would contemplate the divine and beautiful.
So ascending, the soul will come first to The Intelligence and will survey all the beautiful Ideas therein and will avow their beauty, for it is by these ideas that there comes all beauty else, by the offspring and the essence of The Intelligence. What is beyond The Intelligence we affirm to be the nature of the good, radiating beauty before it. (Ennead I, 6, §9)
47
St. Thomas Aquinas
St. Thomas Aquinas (ca. 1225-74) was the great Medieval systematizer of Christian philosophy primarily on the basis of Aristotle, whose work was rediscovered in the West about 1200, having been preserved by the Moslems and transmitted to Europe by Jewish thinkers.
r. xxxix. 8. For beauty there are three requirements. First, a certain wholeness or perfection, for whatever is incomplete is, so far, ugly; second, a due proportion or harmony; and third, clarity, so that brightly coloured things are called beautiful.
a. (2). cxlv. 2. The beauty of the body consists in a man having his bodily members well proportioned, together with a certain appropriate clarity of colour.
s. v. 4. Beauty and goodness are inseparable, for they are based on the same thing, namely the form; and hence what is good is praised as being beautiful. But they are distinguishable; since the good concerns desire and is what all desire, and is therefore conceived as the end, for desire is a kind of impulse towards something. But beauty concerns our cognitive faculty, for those things are called beautiful whose sight pleases. So beauty consists in due proportion, since sense delights in things duly proportioned as in things like to itself. For sense is a kind of correspondence, and so is every power of cognition. And since cognition is by assimilation [of the knower and the known] and assimilation is of the form, beauty belongs strictly to the category of the formal cause.
II. (1). xxvii. i. The beautiful coincides with the good but is distinguishable. For since the good is 'that which all things desire,' it follows from our definition of the good that in it desire should be satisfied. But it is implied in the definition of beauty that by its very sight or recognition desire should be satisfied. Wherefore those senses are most concerned with beauty which are most concerned in apprehension, namely the sight and hearing, which minister to reason. For we speak of beautiful sights and sounds, but do not give the name of beauty to the objects of the other senses, such as tastes or smells. Thus it is clear that beauty affords to our faculty of knowledge something ordered, over and above the good; so that what simply satisfies desire is called good, but that whose very apprehension pleases is called beautiful. (Summa Theologica1267-73.
i. xxxi. 2. Beauty is not essentially' desirable, except so far as it partakes of the essence of the good. And to that extent truth also is desirable. But according to its own essence it has clarity. Commentary on the Sentences 1254-6.
The following short summary of Aquinas' notion of the role of beauty in man's larger cognitive and spiritual quest, by the 20th century British philosopher E.F.Carritt, helps flesh out the theory of knowledge underlying Thomas' brief remarks. (E.F.Carritt, Philosophies of Beauty from Socrates to Robert Bridges, 1931)
48
Ultimate reality cannot be completely known by man, and such knowledge as he can attain of it is not intuitive, but the result of a laborious process of discursive thought. Yet nothing else than a perfect knowledge of it would satisfy him, since what is ultimately real is ultimately good.
But in the immediate perception of some individual sensible objects man attains, without discursive thought, a satisfaction which is analogous, on a small scale, to the complete satisfaction. This is so because the ultimate reality appears through or in the individual sensible object.
The reason why it thus appears in or through some individual sensible objects, is that there is a real difference in these objects, not a difference in man's attitude to them. They are objects where the matter and form or essential character are mutually adequate, so that there is completeness and due proportion of parts, and distinctness like the clarity of colour. Objects which the form thus shines through or illuminates are peculiarly suited to our faculties of perception and are beautiful. So beauty appeals primarily to our intelligence and only incidentally to our practical nature or desires.
Comments on Plato's successors
Plotinus excepted, Plato's successors from Aristotle to the 18th century put
forward ideas about beauty that seem somewhat inconsistent. Each thinker seems
pulled in different directions, as was also the case with Plato. But in the
case of Plato, the divergences seem resolvable. With the others, the divergences
seem too deep, the thinkers too evenly balanced between incompatible ideas.
For example, in Aristotle's remarks about beauty we have seen suggestions of
beauty being an inherent (response-independent) property conflicting with suggestions that it is
a percipient-relational one. In St. Thomas beauty is said to be definable as
that which pleases merely by being seen (heard or otherwise known); this is
plainly a relational conception. But we also have the three requirements of
beauty, namely wholeness, proportionality, and clarity, which seem to be inherent
or percipient-independent properties. The story is much the same for the other
philosophers of the period. For example, for Dionysius the Areopagite, a 6th
century Christian mystic, beauty is both an eternal ideal transcendent of space
and time and also a causal agency in the world, which thereby replicates the
paradox at the heart of Christianity: an eternal God who is also fully incarnate
in the world (at least for a while). And in Leone Ebreo, an early 16th century
humanist, we get a radical suggestion that there is no objective beauty, only
subjective taste, along with other passages that imply that there is an objective
beauty -- as to whose presence in given cases, however, it is very hard to obtain
a consensus.
It is important to understand the incompatibilities in these theories. Consider St. Thomas. The definition he proposes equates beauty with (a species of) cognitive pleasingness. Pleasingness is obviously a matter of response. It is a relation between a thing and a percipient. This is reflected in grammar. The basic linguistic form expressing a relational fact is a transitive verb, in this case X pleases Y. For X to have the property of pleasingness, X must please people or at least have the tendency to do so (which means doing so when the conditions are favorable). Being cognitively pleasing is to be pleasing just on account of being cognized, known -- seen, heard, thought about. Cognitive pleasure is precisely the pleasure one gets in knowing something, apart from anything else about it. So it includes the pleasure of coming to know it and the pleasure of enjoying knowing it. Recall Socrates saying to Phaedrus, "Let me linger over the memory..." Lingerings over the recollection of knowledge give pleasure additional to the pleasure of discovery.
49
Now if beauty is defined in terms of the capacity to give pleasure, beauty is a percipient-relational property, a reponse property, as I have called it. To verify that something is beautiful will require verifying that it produces the relevant hedonic (pleasure-displeasure) response under appropriate conditions. Whatever inherent properties in the object give it the power to produce that response -- whether wholeness, proportionality, and clarity or some other set -- will have to be discovered by empirical investigation. Whatever they turn out to be will not affect the definition. The "essence" of beauty (summed up by the definition) will be its cognitive pleasure-power, not anything percipient-independent in the object itself. Pleasure-power is conceptually primary, the other properties secondary.
On the other hand, if beauty is defined in terms of wholeness and proportionality (let us omit clarity, since it seems likely to be response-related) beauty will be a property which has no essential relatedness to percipients, i.e., a response-independent property. The beauty of anything would necessarily vary with the variation of these properties. In this case, the cognitive pleasure resulting from cognizing things would merely be an effect of beauty, and the wholeness-proportionality would be primary -- i.e. what beauty itself is. It seemed strange to analytically minded philosophers today that these earlier thinkers do not explicitly recognize these differences and frame rationales for choosing among them. One impediment to their doing so was the high respect they felt for their predecessors. This led to the assumption that apparent incompatibilities must be consistent on a deeper level because revered authorities asserted them. Another impediment was the seeming plausibility of each of the incompatible views. Beauty does seem to consist of something in the objects which is there whether or not anyone responds to it. But then again, beauty seems necessarily tied to aesthetic pleasure, hence to percipient response. So one tends to assume that the two ideas must be right, which blinds one to the inconsistency.
Quite apart from the problem of consistency, the idea of cognitive pleasure is worth close attention, since it appears in many theories of beauty. A distinctive pleasure is claimed for cognition, that is, for knowing of various sorts. The case for the pleasures of cognition is typically argued in terms of cognition of the most impressive sort, especially the intuitive intellectual grasp of truths, as in geometry or mathematics. E.F.Carritt, in commenting upon St. Thomas, says that perfect consummation of our innate cognitive drive would be intuitive knowledge of reality as a whole, by which he means Godlike omniscience in which all truths are eternally present to the mind. It is a common theme in ancient writings that this sort of perfection would be gloriously fulfilling. The Theory of Beauty, 1962.
But lesser cognitive accomplishments are also deemed fulfilling. Our senses fulfill themselves in seeing. Thus visual perception is pleasing in proportion as it is successful -- i.e. insofar as we grasp clearly and comprehensively the scene before us. There is an important similarity between perception and intellectual intuition. Perception is intuitive in a certain sense. As in intellectual intuition, an object is immediately present to the mind. It appears in a perceptual image, in living color. It is present rather than represented by a word or an idea, as it must be when we think about it in its absence. In intellectual intuition the object in question is abstract, but there too it is present insofar as the mind grasps it clearly and distinctly, as Descartes put it, to which we may add synoptically (the whole grasped at once). Intuition enables us to dispense with intermediaries like words or symbols. Our common thinking is "discursive" and proceeds piecemeal by such intermediaries. In this it resembles speech or writing. In contrast intellectual intuition seems to bring before us the full reality -- the Platonic Form or the Aristotelian essence -- and consequently to hold in suspension a vast quantity of truth, material enough for many statements. The difference between perception and intellectual intuition is that intuition achieves precise generality impossible to perception (think of geometry), and knows its object more comprehensively than perception can. Given any object of perception there is always endlessly more to discover about it than one can perceive in it at any given time.
50
So, as Carritt says, perception at its best can be reminiscent of intellectual intuition. It is natural to conclude that it produces a somewhat similar pleasure, just on account of being successful, apart from any practical advantage. But one more step is required before we get the conclusion concerning beauty, namely that beauty especially evokes this sort of pleasure. The essential premise here is that certain objects are intrinsically more knowable in the intuitive way, whether in intellectual intuition or perception, and that this superior cognizability is somehow bound up with beauty. In the realm of perception, says Carritt, those concrete particulars whose matter is as compliant with their form as matter can be are both the most (fully, authoritatively) knowable and the most beautiful.
On this explanation, there is supposed to be a correlation between the cognitive pleasure made available by an object and its beauty.
A doubt immediately arises about this idea. Lots of delightful beauties don't seem to be delightful because our cognitive powers are so successful with them. Their beauty is certainly pleasing when we are appreciating them, but if you were to ask, how well do we know them at the moment of greatest appreciation, the answer would often be, not very well. Many beauties are rather mysterious to their adorers, not clearly grasped at all. So it seems.
A possible answer to this objection is that the pleasure we get from beautiful sights and sounds is largely the pleasure of prospective knowledge. They seem so powerfully organized, so intense in some quality or other, that they please in seeming to be well-adapted to premium-grade knowledge. They don't have to be well known at the moment when they are first appreciated. Our cognitive faculties may be attracted by the prospect of future knowledge. So we delight to go on gazing at a beautiful sight. The "splendor" or "aura" of which St. Thomas and others speak may as often be the promise of cognitive success as the fact. Even so, the pleasure felt is a kind of cognitive pleasure -- a pleasure that is taken in prospective cognition.
Our satisfaction in merely looking, without desire to possess or use them, would fit in with this idea. Wanting to behold is certainly connected with wanting to know. Hence aesthetic pleasure may be pleasure taken in knowing and further knowing.
But even when we add prospective pleasure to the theory the problem of variation seems to remain. Even if all aesthetic pleasure involves some actual or expected cognitive pleasure, it is possible that non-cognitive pleasure forms not just some but most of our aesthetic pleasure; and that beauty is as deeply connected with this other pleasure as with the cognitive sorts. Further, even if we could prove that aesthetic pleasure is nothing but cognitive pleasure, we would not have established that beauty can be judged solely by the amount of cognitive pleasure a thing can provide. A large obstacle to any simple equation of beauty and cognitive pleasure-power is the relativity of such power. What has the power to give cognitive pleasure to one person may be powerless to please another. What tacit circumstances are assumed by those who put forward the idea that beauty is power to please? This question will come to the foreground in the next group of theories, those of the 18th century advocates of the sense of beauty.